Question

2．四棱锥P-ABCD中，底面ABCD是平行四边形，点E是PD上的点，且PE=2DE，在PC上找一点F，使得BF∥平面ACE．

Answer 1

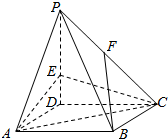
分析 连结BD交AC于O点，连结OE，过B点作OE的平行线交PD于点G，过G作GF∥CE，交PC于点F，连结BF，由此能求出存在点F是PC中点时，使BF∥面AEC．

解答 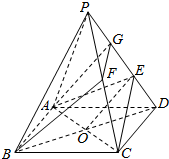解：连结BD交AC于O点，连结OE，过B点作OE的平行线交PD于点G，
过G作GF∥CE，交PC于点F，连结BF．
∵BG∥OE，BG?面AEC，OE?面AEC，
∴BG∥面AEC．
同理GF∥面AEC．
又BG∩GF=G，
∴面BFG∥面AEC，BF?面BFG．
∴BF∥面AEC．
下面求一下点F在PC上的具体位置．
∵BG∥OE，O是BD中点，
∴E是GD中点．
又∵PE：ED=2：1，
∴G是PE中点．
而GF∥CE，∴F为PC中点．
综上，存在点F是PC中点时，使BF∥面AEC．

点评 本题考查满足线面平行的点的位置的确定，是中档题，解题时要认真审题，注意空间思维能力的培养．