
设 是函数
是函数 的一个极值点.
的一个极值点.
(1)求 与
与 的关系式(用
的关系式(用 表示
表示 ),并求
),并求 的单调区间;
的单调区间;
(2)设 ,
, 在区间[0,4]上是增函数.若存在
在区间[0,4]上是增函数.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
(1)b=-3-2a , 当a<-4时f (x) 的减区间有(-∞,3)和(―a―1,+∞),增区间为(3,―a―1); 当a>-4时f (x) 的减区间有(-∞,―a―1)和(3,+∞),增区间为(―a―1,3);
(2)(0, ).
).
【解析】
试题分析:(1)由 是函数
是函数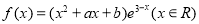 的一个极值点,可得
的一个极值点,可得 ,从而就可用用
,从而就可用用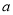 表示出
表示出 来;这样就可以用a的代数式将
来;这样就可以用a的代数式将 表达出来,令其等于零解得两个实根,注意由已知这两个实根应该不等而得到:a≠-4 ,然后通过讨论两根的大小及
表达出来,令其等于零解得两个实根,注意由已知这两个实根应该不等而得到:a≠-4 ,然后通过讨论两根的大小及 的符号就可确定函数
的符号就可确定函数 的单调区间;(2)由(1)可求得当当a>0时,
的单调区间;(2)由(1)可求得当当a>0时, 在区间[0,4]上的最大值和最小值,由已知也可求得
在区间[0,4]上的最大值和最小值,由已知也可求得 在区间[0,4]上的最大值的最小值;而存在
在区间[0,4]上的最大值的最小值;而存在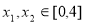 使得
使得 成立等价于
成立等价于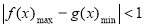 ,解此不等式就可求得
,解此不等式就可求得 的取值范围.
的取值范围.
试题解析:(1)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由 ,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,所以 ,那么a≠-4.
,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,f `(x)<0, f (x)为减函数;
在区间(3,―a―1)上,f `(x)>0,f (x)为增函数;
在区间(―a―1,+∞)上,f `(x)<0,f (x)为减函数.
当a>-4时,x2<3=x1,则
在区间(-∞,―a―1)上,f `(x)<0, f (x)为减函数;
在区间(―a―1,3)上,f (x)>0,f (x)为增函数;
在区间(3,+∞)上,f `(x)<0,f (x)为减函数.
(2)由(Ⅰ)知,当a>0时,f (x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么f (x)在区间[0,4]上的值域是[min{f (0),f (4) },f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又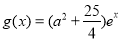 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是[a2+ ,(a2+
,(a2+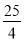 )e4],
)e4],
由于(a2+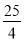 )-(a+6)=a2-a+
)-(a+6)=a2-a+ =(
=( )2≥0,所以只需且仅须
)2≥0,所以只需且仅须
(a2+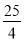 )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a<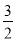 .
.
故a的取值范围是(0, ).
).
考点:1.函数的单调性与极值;2.函数的最值与不等式的存在成立.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:2015届内蒙古高二下学期期末考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,曲线C1的参数方程为  (a>b>0,
(a>b>0, 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M 对应的参数
对应的参数 =
= ,
, 与曲线C2交于点D
与曲线C2交于点D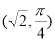
(1)求曲线C1,C2的普通方程;
(2)A(ρ1,θ),Β(ρ2,θ+ )是曲线C1上的两点,求
)是曲线C1上的两点,求  的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com