
为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本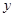 (万元)与处理量
(万元)与处理量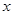 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: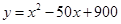 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴 万元.
万元.
(1)当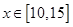 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
(1) 国家最少需要补贴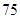 万元,该工厂才能不会亏损;(2)30.
万元,该工厂才能不会亏损;(2)30.
解析试题分析:(1)本题考查函数应用,属于容易题,解题的关键是列出收益函数,收益等于收入减成本,因此有利润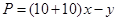 ,化简后它是关于
,化简后它是关于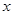 的二次函数,利用二次函数的知识求出
的二次函数,利用二次函数的知识求出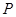 的取值范围,如果
的取值范围,如果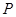 有非负的取值,就能说明可能获利,如果
有非负的取值,就能说明可能获利,如果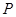 没有非负取值,说明不能获利,而国家最小补贴就是
没有非负取值,说明不能获利,而国家最小补贴就是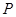 中最大值的绝对值. (2)每吨平均成本等于
中最大值的绝对值. (2)每吨平均成本等于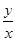 ,由题意
,由题意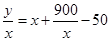 ,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的
,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的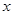 值.
值.
试题解析:(1)根据题意得,利润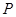 和处理量
和处理量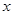 之间的关系:
之间的关系: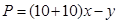
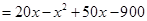
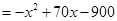 2分
2分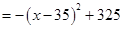 ,
,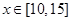 .
.
∵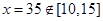 ,
,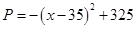 在
在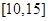 上为增函数,
上为增函数,
可求得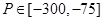 . 5分
. 5分
∴ 国家只需要补贴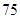 万元,该工厂就不会亏损. 7分
万元,该工厂就不会亏损. 7分
(2)设平均处理成本为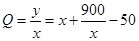 9分
9分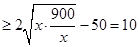 11分
11分
当且仅当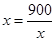 时等号成立,由
时等号成立,由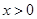 得
得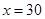 .
.
因此,当处理量为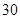 吨时,每吨的处理成本最少为
吨时,每吨的处理成本最少为 万元. 14分
万元. 14分
考点:函数应用题,二次函数的值域,基本不等式的应用.


科目:高中数学 来源: 题型:解答题
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为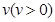 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与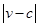 ×S成正比,比例系数为
×S成正比,比例系数为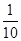 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记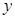 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=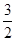 时。
时。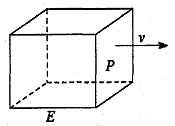
(1)写出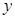 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度 ,使总淋雨量
,使总淋雨量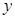 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为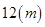 ,高
,高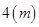 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大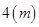 (高不变);二是高度增加
(高不变);二是高度增加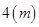 (底面直径不变)。
(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(地面无需用材料);
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本 (万元)可以看成月产量
(万元)可以看成月产量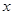 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本 (万元)关于月产量
(万元)关于月产量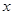 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足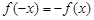 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知函数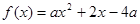
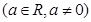 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若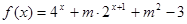 为定义域
为定义域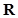 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数a的值.(参考数据:ln2≈0.69,ln10≈2.3)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
修建一个面积为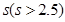 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为 米,修建此矩形场地围墙的总费用为
米,修建此矩形场地围墙的总费用为 元.
元.
(1)求 的表达式;
的表达式;
(2)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com