
分析 (1)当n≥2时,利用an=Sn-Sn-1,然后验证首项;
(2)利用1的结论得到数列{bn} 通项公式,根据公式特点分别利用错位相减法和裂项求和.
解答 解:(1)当n=1时,a1=s1=1;
当n≥2时,an=Sn-Sn-1=$\frac{{n}^{2}+3n}{4}$-$\frac{(n-1)^{2}+3(n-1)}{4}$=$\frac{n+1}{2}$
因为a1=1也适合上式,因此,数列{an}的通项公式为an=$\frac{n+1}{2}$; …(5分)
(2)由(1)知,an=$\frac{n+1}{2}$,
故bn=(n+1)4${\;}^{{a}_{n}}$-$\frac{1}{4{a}_{n}{a}_{n+1}}$=(n+1)4${\;}^{\frac{n+1}{2}}$-$\frac{1}{(n+1)(n+2)}$
=(n+1)2n+1-($\frac{1}{n+1}-\frac{1}{n+2}$),
记A=2×22+3×23+4×24+…+(n+1)2n+1,
2A=2×23+3×24+…n×2n+1+(n+1)2n+2,
两式相减得到-A=2×22+23+24+…2n+1-(n+1)2n+2=-n2n+2,所以A=n2n+2,
B=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n+1}-\frac{1}{n+2}$=$\frac{1}{2}-\frac{1}{n+2}=\frac{n}{2(n+2)}$,
数列{bn}的前n项和为Tn=$n×{2}^{n+2}+\frac{n}{2(n+2)}$.…(12分)
点评 本题考查了数列的通项公式的求法以及利用裂项相消法和错位相减法对数列求和;注意掌握两种求和的通项特征;属于中档题.


科目:高中数学 来源: 题型:解答题
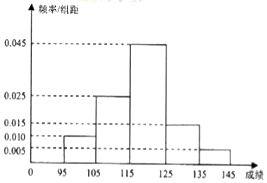 高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.
高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
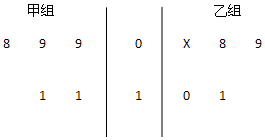 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com