
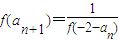 (n∈N*).
(n∈N*).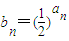 ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,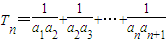 ,试比较Sn与
,试比较Sn与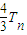 的大小,并加以证明.
的大小,并加以证明.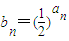 =
=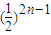 ,知
,知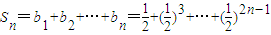 =
=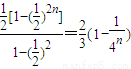 ,
,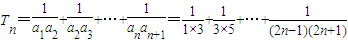 =
=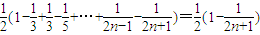 ,所以
,所以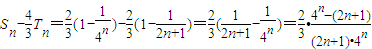 ,欲比较Sn与
,欲比较Sn与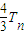 的大小,只需比较4n与2n+1的大小.
的大小,只需比较4n与2n+1的大小. =
=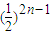 ,
,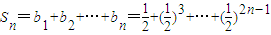 =
=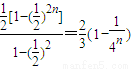 ,
,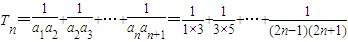 =
=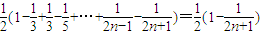 ,…(10分)
,…(10分)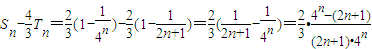 ,
,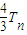 的大小,只需比较4n与2n+1的大小.…(11分)
的大小,只需比较4n与2n+1的大小.…(11分)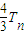 .…(14分)
.…(14分)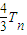 的大小.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
的大小.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化. 

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
| 1 |
| f(-2-an) |
| 1 |
| 2 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:甘肃省月考题 题型:单选题
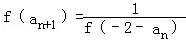 (n∈N*).
(n∈N*).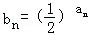 ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,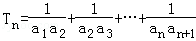 ,试比较Sn与
,试比较Sn与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省张掖二中高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
 (n∈N*).
(n∈N*). ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,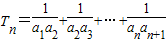 ,试比较Sn与
,试比较Sn与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆八中高三(上)第三次月考数学试卷(文科)(解析版) 题型:解答题
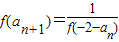 (n∈N*).
(n∈N*). ,Sn=b1+b2+…+bn,
,Sn=b1+b2+…+bn,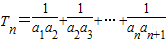 ,试比较Sn与
,试比较Sn与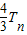 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com