练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，直角△ABC所在平面外一点S，且SA=SB=SC．

    　　(1)求证：点S与斜边AC中点D的连线SD⊥面ABC；

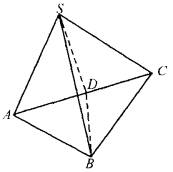
    　　(2)若直角边BA=BC，求证：BD⊥面SAC．

    答案：
    解析：

    		证明：由等腰三角形底边上的中线得到线线垂直，从而得到线面垂直．

    　　(1)在等腰△SAC中，D为AC中点，∴　SD⊥AC如图所示，取AB中点E，连DE、SE

    　　∵　ED∥BC，BC⊥AB，∴　DE⊥AB

    　　又SE⊥AB，∴　AB⊥面SED，∴　AB⊥SD

    　　∴　SD⊥面ABC(AB、AC是面ABC内两相交直线)

    　　(2)∵　BA=BC，BD⊥AC

    　　又∵　SD⊥面ABC，∴　SD⊥BD

    　　∵　SD∩AC=D，∴　BD⊥面SAC


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

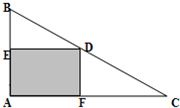    精英家教网Rt△ABC如图所示，直角边|AB|=3，|AC|=4．D点是斜边BC上的动点，DE⊥AB交于点E，DF⊥AC交于点F．设|AE|=x，四边形FDEA的面积为y，求y关于x的函数
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正三棱锥P-ABC的底面边长为6，侧棱长为
    		13
    ．有一动点M在侧面PAB内，它到顶点P的距离与到底面ABC的距离比为2
    		2
    ：1    ．
    精英家教网
    （1）求动点M到顶点P 的距离与它到边AB的距离之比；
    （2）在侧面PAB所在平面内建立为如图所示的直角坐标系，求动点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某小区规划一块周长为2a（a为正常数）的矩形停车场，其中如图所示的直角三角形ADP内为绿化区域．且∠PAC=∠CAB．设矩形的长AB=x，AB＞AD
    （1）求线段DP的长关于x的函数l（x）表达式并指出定义域；
    （2）应如何规划矩形的长AB，使得绿化面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有一矩形钢板ABCD缺损了一角（图中阴影部分），边缘线OM上每一点到点D的距离都等于它到边AB的距离．工人师傅要将缺损的一角切割下来使剩余部分成一个五边形，已知AB=4米，AD=2米．
    （1）如图所示建立直角坐标系，求边缘线OM的轨迹方程；
    （2）①设点P（t，m）为边缘线OM上的一个动点，试求出点P处切线EF的方程（用t表示）；
    ②求AF的值，使截去的△DEF的面积最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

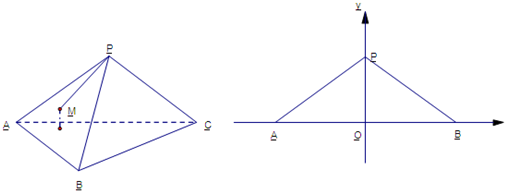
    （2013•永州一模）如图所示，直角梯形ABCD中，∠A=∠D=90°，AD=2，AB=3，CD=4，P在线段AB上，BP=1，O在CD上，且OP∥AD，将图甲沿OP折叠使得平面OCBP⊥底面ADOP，得到一个多面体（如图乙），M、N分别是AC、OP的中点．
    （1）求证：MN⊥平面ACD；
    （2）求平面ABC与底面OPAD所成角（锐角）的余弦值．

    查看答案和解析>>

    同步练习册答案