
(本小题满分12分).设p:实数x满足 ,其中
,其中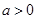 ,命题
,命题 实数
实数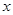 满足
满足 .
.
(I)若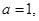 且
且 为真,求实数
为真,求实数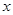 的取值范围;
的取值范围;
(II)若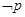 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
(1)2<x<3; (2) 1<a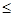 2.
2.
解析试题分析:(1)当a=1时,p真:1<x<3,q真:2<x≤4,由p∧q为真,能求出x的取值范围.
(2)若¬p是¬q的充分不必要条件,则q是p的充分不必要条件,由a>0,知p:a<x<3a,q:2<x≤4,由此能求出a的取值范围。
解:(1)P:(x-1)(x—3)<0, 则1<x<3
q :  则
则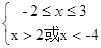 所以2<x
所以2<x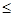 3
3
则  为真,实数
为真,实数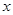 的取值范围 2<x<3
的取值范围 2<x<3
(2) 若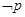 是
是
 的充分不必要条件, 则q是p的充分不必要条件
的充分不必要条件, 则q是p的充分不必要条件
{x|2<x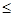 3}
3} {x|a<x<3a}
{x|a<x<3a}
所以a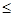 2且3a>3 所以实数a的取值范围1<a
2且3a>3 所以实数a的取值范围1<a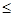 2.
2.
考点:本试题主要考查了复合命题的应用和必要条件、充分条件、充要条件的应用,是基础题.解题时要认真审题,仔细解答.
点评:解决该试题的关键是准确表示命题P,Q的集合,进而利用复合命题的真值问题,结合交集和子集的关系得到结论。


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
命题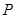 :函数
:函数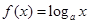 在
在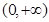 上是增函数;命题
上是增函数;命题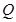 :
: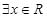 ,使得
,使得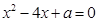 .
.
(1)若命题“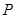 且
且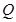 ”为真,求实数
”为真,求实数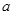 的取值范围;
的取值范围;
(2)若命题“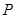 或
或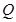 ”为真,“
”为真,“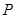 且
且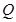 ”为假,求实数
”为假,求实数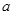 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com