练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设
    a
    =（cosα，sinα），
    b
    =（cosβ，sinβ），则|3
    a
    -4
    b
    |的最大值是（　　）
    分析：利用两个向量的加减法的法则求出向量 3
    a
    -4
    b
     的坐标，要求的式子可化为
    		25-24cos(α-β)
    ，故当cos（α-β）
    =-1 时，要求的式子有最大值为7．
    解答：解：由题意可得  3
    a
    -4
    b
    =（3cosα-4cosβ，3sinα-4sinβ），
    ∴|3
    a
    -4
    b
    |=
    		(3cosα -4cosβ)2+( 3sinα - 4sinβ)2
    =
    		9+16-24cos(α-β)
    =
    		25-24cos(α-β)
    ，
    故当cos（α-β）=-1 时，要求的式子有最大值为7，
    故选C．
    点评：本题考查两个向量的加减法的法则，两个向量坐标形式的运算，求向量的模的方法，求三角函数的最值，把要求的式子
    化为
    		25-24cos(α-β)
    ，是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

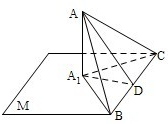    精英家教网已知△ABC的一边BC在平面M内，从A作平面M的垂线，垂足是A1，设△ABC的面积是S，它与平面M组成的二面角等于α（0°＜α＜90°），求证：△A1BC的面积=S•cosα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•崇明县一模）设函数f(x)=cos(2x+
    π
    3
    )+sin2x    ．
    （1）求函数f（x）的最大值和最小正周期；
    （2）设A，B，C为△ABC的三个内角，f(
    C
    2
    )=-
    1
    4
    ，且C为锐角，S△ABC=5
    		3
    ，a=4，求c边的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文）设函数f(x)=cos(2x+
    π
    3
    )+
    		3
    sin2x    ．
    （1）求函数f（x）的最大值和及相应的x的值；
    （2）设A，B，C为△ABC的三个内角，f(
    C
    2
    -
    π
    12
    )=
    		3
    2
    ，S△ABC=5
    		3
    ，a=4    ，求角C的大小及b边的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

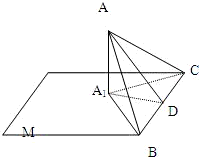    已知△ABC的一边BC在平面M内，从A作平面M的垂线，垂足是A1，设△ABC的面积是S，它与平面M组成的二面角等于α（0°＜α＜90°），求证：△A1BC的面积=S•cosα．

    查看答案和解析>>

    科目：高中数学 来源：1961年全国统一高考数学试卷（解析版） 题型：解答题

    已知△ABC的一边BC在平面M内，从A作平面M的垂线，垂足是A1，设△ABC的面积是S，它与平面M组成的二面角等于α（0°＜α＜90°），求证：△A1BC的面积=S•cosα．

    查看答案和解析>>

    同步练习册答案