Question

2．已知△ABC的外接圆的圆心为O，若$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$，且|${\overrightarrow{AC}}$|=|${\overrightarrow{AO}}$|，则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为150°．

Answer 1

分析 利用两个向量的加减法的法则，以及其几何意义，求得$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角．

解答 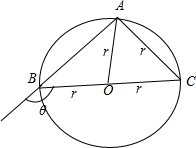解：△ABC的外接圆的圆心为O，设$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为θ，
∵$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$，∴O为线段BC的中点，故BC为直径．
∵|${\overrightarrow{AC}}$|=|${\overrightarrow{AO}}$|=r（r为△ABC的外接圆的半径），
∴△AOC为等边三角形，
∴∠AOC=60°，∠AOB=120°．
又△OAB为等腰三角形，故∠OAB=∠OBA=30°，
设$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为θ，则θ=180-∠AOB=150°
故答案为：150°．

点评 本题主要考查两个向量的加减法的法则，以及其几何意义，属于基础题．