练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设
    π
    3
    ＜α＜
    3π
    4
    ，sin(α-
    π
    4
    )=
    3
    5
    ，则
    sinα-cos2α+1    
    tanα
    的值为
    5
    		2
    +14
    50
    5
    		2
    +14
    50
    ．
    分析：首先根据角的范围以及同角三角函数的基本关系求出cos（α-
    π
    4
    ）、sinα、cosα的值，然后利用二倍角公式化简所求的式子，并将相应的值代入即可．
    解答：解：∵
    π
    3
    ＜α＜
    3π
    4
    ，
    ∴
    π
    12
    ＜α-
    π
    4
    ＜
    π
    2

    ∵sin(α-
    π
    4
    )=
    3
    5

    ∴cos（α-
    π
    4
    ）=
    		1-sin2(α-
    π
    4
    )
    =
    4
    5
    ．
    ∴sinα=sin[（α-
    π
    4
    ）+
    π
    4
    ]
    =sin（α-
    π
    4
    ）cos
    π
    4
    +cos（α-
    π
    4
    ）sin
    π
    4

    =
    3
    5
    ×
    		2
    2
    +
    4
    5
    ×
    		2
    2
    =
    7
    		2
    10

    ∴cosα=
    		1-sin2α
    =
    		2
    10

    tanα=
    sinα
    cosα
    =7
    ∴
    sinα-cos2α+1
    tanα

    =
    sinα+2sin2α
    tanα

    =
    sinα(1+2sinα)
    sinα
    cosα

    =cosα（1+2sinα）
    =
    		2
    10
    （1+2×
    7
    		2
    10
    ）
    =
    5
    		2
    +14
    50
    ．
    故答案为：
    5
    		2
    +14
    50
    ．
    点评：本题主要考查同角三角函数的基本关系、二倍角公式等，求出sinα是解题的关键，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设
    π
    2
    ＜x＜
    3π
    4
    ，令a=sinx，b=cosx，c=tanx，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f，g都是由A到A的映射，其对应法则如下表（从上到下）：
    表1  映射f的对应法则
    原像 1 2 3 4
    像 3 4 2 1
    表2  映射g的对应法则
    原像 1 2 3 4
    像 4 3 1 2
    则与f[g（1）]相同的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2014届江苏省高二下学期期中考试数学文科试卷（解析版） 题型：解答题

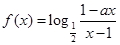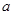    )设为奇函数，为常数．

    (1)求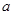的值；

    (2)判断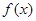在区间（1，＋∞）内的单调性，并证明你的判断正确；

    (3)若对于区间 [3,4]上的每一个的值，不等式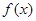>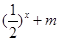恒成立，求实数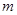的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A＝{1,2,3,4,5},B={6,7,8}，记从A到B的映射为f:AB,x∈A,求：

    （1）满足B中元素都有原象的映射f的个数；

    （2）满足x+f(x)都为偶数的映射f的个数;

    （3）满足f(1)≤f(2)≤f(3)≤f(4)≤f(5)的映射f的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合U={1,2,3,4,5},A={1,2,3},B={3,4,5}，则等于(    ).

    A.{1，2，3，4}                   B.{1，2，5}

    C.{1，2，4，5}                   D.{3}

    查看答案和解析>>

    同步练习册答案