
 已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$.
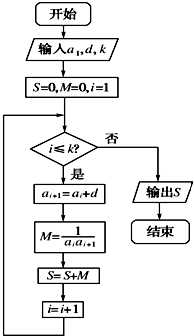
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$.分析 (1)根据程序框图分析程序功能,利用裂项相消法,求出数列的首项和公式,可得答案;
(2)利用错位相减法,结合(1)中结论,可得{bn}的前n项和为Tn.
解答 解:(1)由框图可知该程序的功能是,计算并输出 S=$\frac{1}{{a}_{1}•{a}_{2}}$+$\frac{1}{{a}_{2}•{a}_{3}}$+…+$\frac{1}{{a}_{k}•{a}_{k+1}}$的值,…(2分)
∵{an}是等差数列,其公差为d,则有$\frac{1}{{a}_{k}•{a}_{k+1}}$=$\frac{1}{d}$($\frac{1}{{a}_{k}}$-$\frac{1}{{a}_{k+1}}$),
∴S=$\frac{1}{d}$($\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{k}}$-$\frac{1}{{a}_{k+1}}$)=$\frac{1}{d}$($\frac{1}{{a}_{1}}-\frac{1}{{a}_{k+1}}$),…(4分)
由题意可知,k=5时,S=$\frac{5}{11}$;
k=10时,S=$\frac{10}{21}$;
即$\frac{1}{d}$($\frac{1}{{a}_{1}}-\frac{1}{{a}_{6}}$)=$\frac{5}{11}$;$\frac{1}{d}$($\frac{1}{{a}_{1}}-\frac{1}{{a}_{11}}$)=$\frac{10}{21}$,
解得$\left\{\begin{array}{l}{a}_{1}=2\\ d=2\end{array}\right.$,或$\left\{\begin{array}{l}{a}_{1}=-1\\ d=-2\end{array}\right.$(舍去) …(6分)
∴an=2n; …(7分)
(2)∵bn=(n+1)•2${\;}^{{a}_{n}}$=(n+1)•4n,
∴Tn=2•41+3•42+4•43+…+(n+1)•4n,
4Tn=2•42+3•43+4•44+…+(n+1)•4n+1,
两式相减得:
-3Tn=2•41+42+43+…+4n-(n+1)•4n+1
=4+$\frac{4(1-{4}^{n})}{1-4}$-(n+1)•4n+1
=$\frac{8}{3}$-(n+$\frac{2}{3}$)•4n+1,
∴Tn=$(\frac{3n-2}{9})$•4n+1-$\frac{8}{9}$,
点评 本题考查的知识点是数列求和,熟练掌握裂项相消法和错位相减法求和的方法步骤,是解答的关键.


科目:高中数学 来源: 题型:解答题
| 男 | 女 | |
| 愿意做 | 40 | 30 |
| 不愿意做 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n<m | B. | n>m | C. | n=m | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(理)试卷(解析版) 题型:解答题
已知椭圆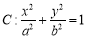
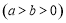 的焦距为2,离心率为
的焦距为2,离心率为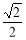 ,
,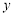 轴上一点
轴上一点 的坐标为
的坐标为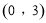 .
.
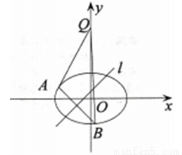
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线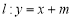 ,椭圆
,椭圆 上总存在不同的两点
上总存在不同的两点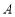 与
与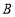 关于直线
关于直线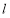 对称,且
对称,且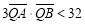 ,求
,求
实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲

如图,过圆内接四边形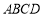 的顶点
的顶点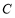 引切线
引切线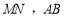 为圆的直径.
为圆的直径.
(Ⅰ)若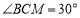 ,求
,求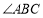 ;
;
(Ⅱ)已知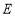 为线段
为线段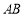 上一点,满足
上一点,满足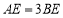 ,
,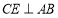 ,求证:
,求证: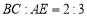 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com