
| 男 | 女 | |
| 愿意做 | 40 | 30 |
| 不愿意做 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析 (1)由列联表可知调查的500名志愿者中有70名志愿者愿意做微商,两个数据求比值得到该地区志愿者中,愿意做微商的比例的估算值.
(2)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,看出有99.9%的把握认为该地区的志愿者是否需要愿意做微商与性别有关.
解答 解:(1)调查的500名志愿者中有70名志愿者愿意做微商,因此该地区志愿者中,愿意做微商的比例的估算值为$\frac{70}{500}$=14%--------------------------------------(5分)
(2)K2=$\frac{500×(40×270-30×160)^{2}}{200×300×70×430}≈9.967$.
由于9.967>6.635,所以有99.9%的把握认为该地区的志愿者是否需要愿意做微商与性别有关.-------------(12分)
点评 本题主要考查统计学知识,考查独立性检验的思想,考查利用数学知识研究实际问题的能力以及相应的运算能力.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x=0或x≥1} | C. | {0,1} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{3}$)∪(0,+∞) | B. | (-$\frac{1}{6}$,+∞) | C. | (-∞,-$\frac{1}{3}$)和(0,+∞) | D. | (-∞,-$\frac{1}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递增,是偶函数 | B. | 单调递减,是偶函数 | ||
| C. | 单调递增,是奇函数 | D. | 单调递减,是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
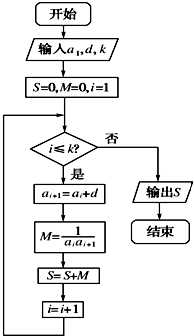 已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$.
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com