
已知函数 ,(
,(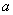 为常数,
为常数,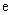 为自然对数的底).
为自然对数的底).
(Ⅰ)当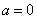 时,求
时,求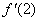 ;
;
(Ⅱ)若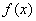 在
在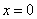 时取得极小值,试确定
时取得极小值,试确定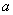 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设由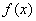 的极大值构成的函数为
的极大值构成的函数为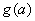 ,将
,将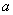 换元为
换元为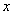 ,试判断曲线
,试判断曲线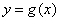 是否能与直线
是否能与直线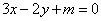 (
( 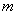 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由.
科目:高中数学 来源: 题型:
国家环境标准制定的空气质量指数与空气质量等级对应关系如下表:
| 空气质量指数 | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如下:
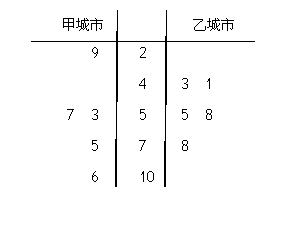
(Ⅰ)试根据上面的统计数据,判断甲、乙两个城市的空气质量指数的方差的大小关系(只需写出结果);
(Ⅱ)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(Ⅲ)分别从甲城市和乙城市的统计数据中任取一个,试求这两个城市空气质量等级相同的概率.
(注: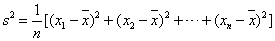 ,其中
,其中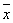 为数据
为数据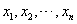 的平均数.)
的平均数.)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
A.y=0.8x+3 B.y=-1.2x+7.5
C.y=1.6x+0.5 D.y=1.3x+1.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com