
(本题满分16分)A、B是函数f(x)=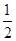 +
+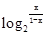 的图象上的任意两点,且
的图象上的任意两点,且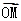 =
=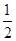 (
(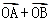 ),已知点M的横坐标为
),已知点M的横坐标为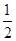 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(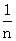 )+f(
)+f(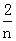 )+…+f(
)+…+f(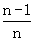 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为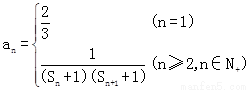 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<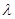 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数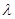 的取值范围.
的取值范围.
(Ⅰ)证明:设A(x1,y1),B(x2,y2),M(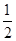 ,ym),由
,ym),由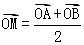 得
得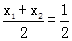
即x1+x2=1.
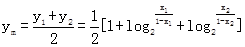
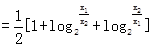
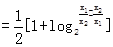
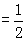
即M点的纵坐标为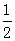 . …………………………………………………4分
. …………………………………………………4分
(Ⅱ)当n≥2时,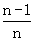 ∈(0,1),又
∈(0,1),又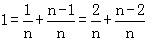 =…=x1+x2,
=…=x1+x2,
∴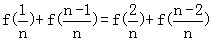 =…=f(x1)+f(x2)=y1+y2=1.
=…=f(x1)+f(x2)=y1+y2=1.
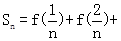 …
…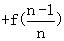 ,又
,又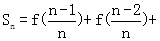 …
…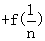 ,
,
∴2Sn=n-1,则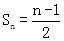 (n≥2,n∈N+). ……………………………10分
(n≥2,n∈N+). ……………………………10分
(Ⅲ)由已知T1=a1=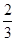 ,n≥2时,
,n≥2时,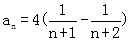 ,
,
∴Tn=a1+a2+…+an=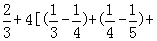 …
…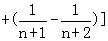 =
=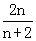 .
.
当n∈N+时,Tn<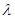 (Sn+1+1),即
(Sn+1+1),即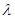 >
>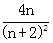 ,n∈N+恒成立,则
,n∈N+恒成立,则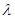 >
>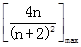 .
.
而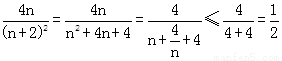 (n=2时“=”成立),
(n=2时“=”成立),
∴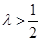 ,∴实数
,∴实数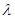 的取值范围为(
的取值范围为(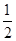 ,+∞). ……………………16分
,+∞). ……………………16分
【解析】略


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
查看答案和解析>>
科目:高中数学 来源:2012届江苏省泰州中学高三上学期期中考试数学 题型:解答题
(本题满分16分)A、B是函数f(x)= +
+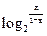 的图象上的任意两点,且
的图象上的任意两点,且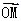 =
= (
(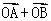 ),已知点M的横坐标为
),已知点M的横坐标为 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f( )+f(
)+f( )+…+f(
)+…+f(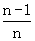 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为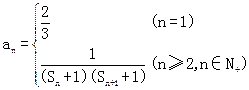 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<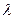 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数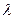 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高级中高三第二次月考试卷数学 题型:解答题
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
(1)求实数m的值,并写出区间D;
(2)若底数 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011年安徽省淮安五校高一上学期期末考试数学试卷 题型:解答题
(本题满分16分)已知ABCD四点的坐标分别为 A(1,0), B(4,3),
C(2,4),D(0,2)
⑴证明四边形ABCD是梯形;
⑵求COS∠DAB。
⑶设实数t满足( -t
-t )·
)· =0,求t的值。
=0,求t的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com