
| A. | 梯形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 先根据条件可判断四边形ABCD是平行四边形,而根据$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|$得出$|\overrightarrow{AC}|=|\overrightarrow{BD}|$,这便说明平行四边形ABCD的对角线相等,从而便可得出四边形ABCD的形状.
解答 解:∵$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$;
∴四边形ABCD是平行四边形;
如图,$\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{a}-\overrightarrow{b}$;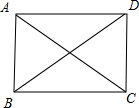
且$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b},|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|$;
∴$|\overrightarrow{AC}|=|\overrightarrow{DB}|$;
∴平行四边形ABCD是矩形.
故选B.
点评 考查向量加法的平行四边形法则,向量减法的几何意义,以及矩形的概念.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 23 | C. | 34 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
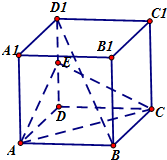 如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 14 | 18 | 19 | 20 | 23 | 25 | 28 |
| A. | 一次函数模型 | B. | 二次函数模型 | C. | 指数函数模型 | D. | 对数函数模型 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
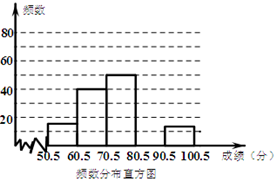 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com