练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在中，角的对边分别为，且，若的面积为，则的最小值为（ ）

    A.B.C.D.3

    【答案】B

    【解析】

    试题由正弦定理，有，又2c·cosB＝2a＋b，得

    2sinC·cosB＝2sin A＋sinB，

    由A＋B＋C＝π，得sin A＝sin(B＋C)，

    则2sinC·cosB＝2sin(B＋C)＋sinB，即2sinB·cosC＋sinB＝0，

    又0＜B＜π，sinB＞0，得cosC＝－，

    因为0＜C＜π，得C＝，

    则△ABC的面积为S△＝ab sinC＝ab，即c＝3ab，

    由余弦定理，得c2＝a2＋b2－2ab cosC，化简，得a2＋b2＋ab＝9a2b2，

    ∵a2＋b2≥2ab，当仅当a=b时取等号，

    ∴2ab＋ab≤9a2b2，即ab≥，故ab的最小值是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】动点到定点的距离比它到直线的距离小1，设动点的轨迹为曲线，过点的直线交曲线于、两个不同的点，过点、分别作曲线的切线，且二者相交于点.

    （1）求曲线的方程；

    （2）求证： ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A、B是单位圆O上的两点（O为圆心），∠AOB=120°，点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径，则的取值范围是（ ）

    A. [，0） B. [，0] C. [，1） D. [，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在区间上有最大值和最小值.设

    （1）求的值

    （2）若不等式在上有解,求实数的取值范围;

    （3）若有三个不同的实数解,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}满足：①a1=1；②所有项an∈N*；③1=a1<a2<…<an<an+1<….设集合Am={n|an≤m，m∈N*），将集合Am中的元素的最大值记为bm，即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值.我们称数列{bn}为数列{an}的伴随数列.

    例如，数列1，3，5的伴随数列为1，1，2，2，3.

    （I）若数列{an}的伴随数列为1，1，2，2，2，3，3，3，3……，请写出数列{an}；

    （II）设an=4n-1，求数列{an}的伴随数列{bn}的前50项之和；

    （III）若数列{an}的前n项和（其中c为常数），求数列{an}的伴随数列{bm}的前m项和Tm.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在推导很多三角恒等变换公式时，我们可以利用平面向量的有关知识来研究，在一定程度上可以简化推理过程.如我们就可以利用平面向量来推导两角差的余弦公式:

    具体过程如下：

    如图，在平面直角坐标系内作单位圆O，以为始边作角.它们的终边与单位圆O的交点分别为A，B.

    则

    由向量数量积的坐标表示，有：

    设的夹角为θ，则

    另一方面，由图3.1—3（1）可知，；由图可知，

    .于是.

    所以，也有，

    所以，对于任意角有：（）

    此公式给出了任意角的正弦、余弦值与其差角的余弦值之间的关系，称为差角的余弦公式，简记作.

    有了公式以后，我们只要知道的值，就可以求得的值了.

    阅读以上材料，利用下图单位圆及相关数据（图中M是AB的中点），采取类似方法（用其他方法解答正确同等给分）解决下列问题：

    （1）判断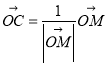是否正确？（不需要证明）

    （2）证明：

    （3）利用以上结论求函数的单调区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

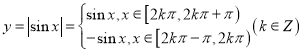    【题目】（一）在函数图象的学习中常常用到化归转化的思想，往往通过对一些已经学习过的函数图象的研究，进一步迁移到其它函数，例如函数与正弦函数就有密切的联系，因为.只需将在轴下方的图象翻折到上方，就得到的图象.

    （二）在研究函数零点问题时，往往会将函数零点问题转化为两个函数图象的交点问题.例如研究函数的零点就可以转化为函数与函数的图象交点来进行处理，通过作图不仅知道函数有且仅有一个零点，还可以确定零点.这体现了化归转化与数形结合的思想在函数研究中的应用.

    结合阅读材料回答下面两个问题：

    作出函数的图象；

    利用作图的方法验证函数有且仅有两个零点.若记两个零点分别为，，证明：.（注：在同一坐标中作图）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72，108，120人，现采用分层抽样的方法，从该单位上述员工中抽取25人调查专项附加扣除的享受情况.

    项目

    员工

    A

    B

    C

    D

    E

    F

    子女教育

    ○

    ○

    ×

    ○

    ×

    ○

    继续教育

    ×

    ×

    ○

    ×

    ○

    ○

    大病医疗

    ×

    ×

    ×

    ○

    ×

    ×

    住房贷款利息

    ○

    ○

    ×

    ×

    ○

    ○

    住房租金

    ×

    ×

    ○

    ×

    ×

    ×

    赡养老人

    ○

    ○

    ×

    ×

    ×

    ○

    （1）应从老、中、青员工中分别抽取多少人？

    （2）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为A，B，C，D，E，F.享受情况如下表，其中“○”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.

    ①试用所给字母列举出所有可能的抽取结果；

    ②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”，求事件M发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为F1、F2，离心率为，且经过点.

    （1）求椭圆C的方程；

    （2）动直线与椭圆C相交于点M，N，椭圆C的左右顶点为,直线与相交于点，证明点在定直线上，并求出定直线的方程.

    查看答案和解析>>

    同步练习册答案