
【题目】已知函数 ![]() .(Ⅰ)求函数
.(Ⅰ)求函数 ![]() 的最小正周期及单调递增区间;(Ⅱ)将
的最小正周期及单调递增区间;(Ⅱ)将 ![]() 的图像向右平移
的图像向右平移 ![]() 个单位得到函数
个单位得到函数 ![]() 的图像,若
的图像,若 ![]() ,求函数
,求函数 ![]() 的值域.
的值域.
【答案】解:(Ⅰ)f(x)=cosx( ![]() sinx+cosx)+1
sinx+cosx)+1
=cos2x+ ![]() sinxcosx+1
sinxcosx+1 ![]()
= ![]() cos2x+
cos2x+ ![]() sin2x+
sin2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]()
∵T= ![]() =
= ![]() =
= ![]()
即函数f(x)的最小正周期为 ![]() .
.
由f(x)=sin(2x+ ![]() )+
)+ ![]()
由2k ![]() -
- ![]() ≤2x+
≤2x+ ![]() ≤2k
≤2k ![]() +
+ ![]() ,
, ![]()
解得:- ![]() +k
+k ![]() ≤x≤
≤x≤ ![]() +k
+k ![]() ,
, ![]()
故函数f(x)=sin(2x+ ![]() )+
)+ ![]() 的单调递增区间为[-
的单调递增区间为[- ![]() +k
+k ![]() ,
, ![]() +k
+k ![]() ],
], ![]() .
.
(Ⅱ) ![]() ,x
,x ![]() [-
[- ![]() ,
, ![]() ],-
],- ![]() ≤2x≤
≤2x≤ ![]() ,
,
∴- ![]() ≤
≤ ![]() ≤1
≤1
∴函数的值域为 ![]()
【解析】(1)首先通过三角函数的二倍角正余弦公式![]() 恒等变换把三角函数的关系式变形成正弦函数进一步利用三角函数的性质求出函数的周期和单调区间。(2)利用(1)的结论进一步利用函数的定义域求出三角函数的值域。
恒等变换把三角函数的关系式变形成正弦函数进一步利用三角函数的性质求出函数的周期和单调区间。(2)利用(1)的结论进一步利用函数的定义域求出三角函数的值域。


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】设 ![]() 是两条不同的直线,
是两条不同的直线, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ![]() ,则
,则 ![]() ②若
②若 ![]() ,则
,则 ![]()
③若 ![]() ,则
,则 ![]() ④若
④若 ![]() ,则
,则 ![]()
其中正确命题的序号是( )
A.①和②
B.②和③
C.③和④
D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知N为自然数集,集合P={1,4,7,10,13},Q={2,4,6,8,10},则P∩ ![]() 等于( )
等于( )
A.{1,7,13}
B.{4,10}
C.{1,7}
D.{0,1,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)若曲线y=f(x)在P(1,f(1))处的切线平行于直线y=﹣x+1,求函数y=f(x)的单调区间;
(2)若a>0,且对任意x∈(0,2e]时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,平面PAD⊥ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
中,平面PAD⊥ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.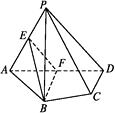
求证:
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com