
设函数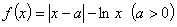 .
.
(1)若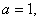 求
求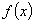 的单调区间及
的单调区间及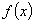 的最小值;
的最小值;
(2)若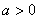 ,求
,求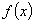 的单调区间;
的单调区间;
(3)试比较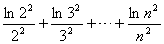 与
与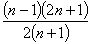 的大小.
的大小.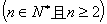 ,并证明你的结论.
,并证明你的结论.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
设函数f(x)=x2-2x+3,g(x)=x2-x
(1)解不等式|f(x)-g(x)|≥2 014;
(2)若|f(x)-a|<2恒成立的充分条件是1≤x≤2,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
某学生在一门功课的22次考试中,所得分数茎叶图如右所示,则此学生该门功课考试分数的极差与中位数之和为
A.117 B.118 C.118.5 D.119.5
|
查看答案和解析>>
科目:高中数学 来源: 题型:
采用系统抽样方法从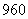 人中抽取
人中抽取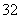 人做问卷调查,为此将他们随机编号为
人做问卷调查,为此将他们随机编号为 ,
,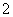 ,……,
,……,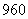 ,分组后在第一组采用简单随机抽样的方法抽到的号码为
,分组后在第一组采用简单随机抽样的方法抽到的号码为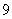 .抽到的
.抽到的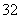 人中,编号落入区间
人中,编号落入区间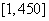 的人做问卷
的人做问卷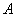 ,编号落入区间
,编号落入区间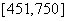 的人做问卷
的人做问卷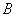 ,其余的人做问卷
,其余的人做问卷 .则抽到的人中,做问卷
.则抽到的人中,做问卷 的人数为 ( )
的人数为 ( )

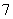
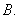
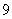
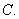
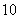
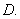
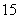
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com