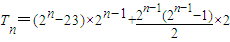Question

将等差数列{a_n}的所有项依次排列，并如下分组：（a₁），（a₂，a₃），（a₄，a₅，a₆，a₇），…，其中第1组有1项，第2组有2项，第3组有4项，…，第n组有2^n-1项，记T_n为第n组中各项的和，已知T₃=-48，T₄=0，
（I）求数列{a_n}的通项公式；
（II）求数列{T_n}的通项公式；
（III）设数列{ T_n }的前n项和为S_n，求S₈的值．

Answer 1

【答案】分析：（I）设{a_n}的公差为d，则T₃=4a₇-6d=-48，T₄=8a₇+36d=0，由此能够求出{a_n}的通项公式．
（II）当n≥2时，在前n-1组中共有项数为1+2+…+2^n-2=2^n-1-1，由此能求出数列{T_n}的通项公式．
（III）由S₈为数列{a_n}前8组元素之和，且这8组总共有255项，由此能求出S₈的值．
解答：解：（I）设{a_n}的公差为d，
由题意T₃=4a₇-6d=-48①，
T₄=8a₇+36d=0②，
解①、②得d=2，a₇=-9，
∴a_n=2n-23；
（II）当n≥2时，在前n-1组中共有项数为：1+2+…+2^n-2=2^n-1-1，
故第n组中的第一项是{a_n}中的第2^n-1项，且第n组中共有2^n-1项，
∴第n组中的2^n-1项的和：

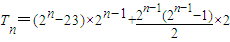
=3×2^2n-2-24×2^n-1．
当n=1时，T₁=a₁=-21适合上式，
∴T_n=3×2^2n-2-24×2^n-1．
（III）∵S₈=T₁+T₂+T₃+…+T_n，
即数列{a_n}前8组元素之和，且这8组总共有1+2+2²+…+2⁷=2⁸-1=255，
∴S₈=255
=255×（-21）+
=59415．
点评：本题考查数列的通项公式的求法，设数列{ T_n }的前n项和为S_n，求S₈的值．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．