
(09年西城区抽样理)(14分)
已知![]() 的顶点A在射线
的顶点A在射线![]() 上, A, B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足
上, A, B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足![]() . 当点A在l上移动时,记点M的轨迹为W.
. 当点A在l上移动时,记点M的轨迹为W.
(Ⅰ) 求轨迹W的方程;
(Ⅱ)设P(-1,0),Q(2,0),求证: 解析:(Ⅰ)解:因为A, B两点关于x轴对称,![]()
所以AB边所在直线与y轴平行.
设M(x, y),由题意,得![]() , ----------------------2分
, ----------------------2分
所以![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() , ------------------------5分
, ------------------------5分
所以点M的轨迹W的方程为![]() . ------------------6分
. ------------------6分
(Ⅱ)证明:设![]() ,
,
因为曲线![]() 关于x轴对称,
关于x轴对称,
所以只要证明“点M在x轴上方及x轴上时,![]() ”成立即可.
”成立即可.
以下给出“当![]() 时,
时,![]() ” 的证明过程.
” 的证明过程.
因为点M在![]() 上,所以
上,所以![]() .
.
当x0=2时,由点M在W上,得点![]() ,
,
此时![]() ,
,
所以![]() ,则
,则![]() ; --------------8分
; --------------8分
当![]() 时,直线PM、QM的斜率分别为
时,直线PM、QM的斜率分别为![]() ,
,
因为![]() ,所以
,所以![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]()
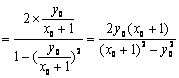 ,--10分
,--10分
因为点M在W上,所以![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
因为![]() ,
,
所以![]() , --------------------12分
, --------------------12分
在![]() 中,因为
中,因为![]() ,且
,且![]() ,
,![]() ,
,
所以![]() .
.
综上,得当![]() 时,
时,![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
(09年西城区抽样理)(14分)
已知f是直角坐标平面xOy到自身的一个映射,点![]() 在映射f下的象为点
在映射f下的象为点![]() ,记作
,记作![]() .
.
设![]()
![]() ,
,![]() ,
,![]() . 如果存在一个圆,使所有的点
. 如果存在一个圆,使所有的点![]() 都在这个圆内或圆上,那么称这个圆为点
都在这个圆内或圆上,那么称这个圆为点![]() 的一个收敛圆. 特别地,当
的一个收敛圆. 特别地,当![]() 时,则称点
时,则称点![]() 为映射f下的不动点.
为映射f下的不动点.
(Ⅰ) 若点![]() 在映射f下的象为点
在映射f下的象为点![]() .
.
1 求映射f下不动点的坐标;
2 若![]() 的坐标为(1,2),判断点
的坐标为(1,2),判断点![]() 是否存在一个半径为3的收敛圆,并说明理由.
是否存在一个半径为3的收敛圆,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样理)(14分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(![]() R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(Ⅰ)设![]() ,若h (x)为偶函数,求
,若h (x)为偶函数,求![]() ;
;
(Ⅱ)设![]() ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
(Ⅲ)试判断h(x)能否为任意的一个二次函数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样理)(14分)
已知数列![]() 的前n项和为Sn,a1=1,数列
的前n项和为Sn,a1=1,数列![]() 是公差为2的等差数列.
是公差为2的等差数列.
(Ⅰ)求![]() ;
;
(Ⅱ)证明数列![]() 为等比数列;
为等比数列;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样理)(12分)
在甲、乙两个批次的某产品中,分别抽出3件进行质量检验. 已知甲、乙批次每件产品检验不合格的概率分别为![]() ,假设每件产品检验是否合格相互之间没有影响.
,假设每件产品检验是否合格相互之间没有影响.
(Ⅰ)求至少有2件甲批次产品检验不合格的概率;
(Ⅱ)求甲批次产品检验不合格件数恰好比乙批次产品检验不合格件数多1件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com