
【题目】设数列{an}的前n项和为Sn , 且an=2﹣2Sn , 数列{bn}为等差数列,且b5=14,b7=20.
(1)求数列{an}的通项公式;
(2)若cn=anbn , n∈N* , 求数列{cn}的前n项和Tn .
【答案】
(1)解:∵an=2﹣2Sn,当n=1时,a1=2﹣2a1,解得a1= ![]() ;
;
当n≥2时,an﹣1=2﹣2Sn﹣1,
∴an﹣an﹣1=2﹣2Sn﹣(2﹣2Sn﹣1)=﹣2an,
化为3an=an﹣1,
∴数列{an}是等比数列,首项为 ![]() ,公比为
,公比为 ![]() ,
,
可得:an= ![]() (
( ![]() )n﹣1=2(
)n﹣1=2( ![]() )n,n∈N*
)n,n∈N*
(2)解:数列{bn}为等差数列,公差为d且b5=14,b7=20.
可得b1+4d=14,b1+6d=20,
解得b1=2,d=3,
可得bn=b1+(n﹣1)d=2+3(n﹣1)=3n﹣1,n∈N*;
cn=anbn=2(3n﹣1)( ![]() )n.
)n.
前n项和Tn=2[2( ![]() )+5(
)+5( ![]() )2+7(
)2+7( ![]() )3+…+(3n﹣1)(
)3+…+(3n﹣1)( ![]() )n],
)n],
![]() Tn=2[2(
Tn=2[2( ![]() )2+5(
)2+5( ![]() )3+7(
)3+7( ![]() )4+…+(3n﹣1)(
)4+…+(3n﹣1)( ![]() )n+1],
)n+1],
相减可得 ![]() Tn=2[
Tn=2[ ![]() +2(
+2( ![]() )2+2(
)2+2( ![]() )3+…+2(
)3+…+2( ![]() )n﹣(3n﹣1)( )n+1]
)n﹣(3n﹣1)( )n+1]
=2[ ![]() +2
+2 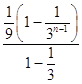 ﹣(3n﹣1)(
﹣(3n﹣1)( ![]() )n+1],
)n+1],
化简可得Tn= ![]() ﹣
﹣ ![]()
【解析】(1)由数列的递推式:当n=1时,a1=S1,当n≥2时,an=Sn﹣Sn﹣1,即可得到数列{an}的通项公式;(2)数列{bn}为等差数列,公差为d,运用等差数列的通项公式,结合条件,解方程可得首项和公差,即可得到bn,求出cn=anbn=2(3n﹣1)( ![]() )n.运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理,即可得到所求和.
)n.运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理,即可得到所求和.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列所给4个图像中,与所给3件事吻合最好的顺序为( )
(1.)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2.)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3.)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.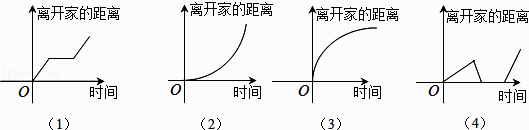
A.(4)(1)(2)
B.(4)(2)(3)
C.(4)(1)(3)
D.(1)(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 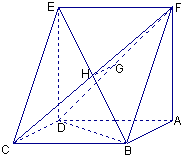
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足(2b﹣c)cosA﹣acosC=0.
(1)求角A的大小;
(2)若a=4,求△ABC周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通项公式;
(Ⅱ)设cn=an+bn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com