
 ,E、F分别是线段AC、AD的中点,连接BE、EF、FB、BD.
,E、F分别是线段AC、AD的中点,连接BE、EF、FB、BD.
 =(1,0,1),利用向量的夹角公式,即可求直线BD与平面BEF所成的角的大小.
=(1,0,1),利用向量的夹角公式,即可求直线BD与平面BEF所成的角的大小.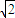
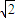 ,AD=
,AD=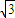 ,∴AD2=AC2+DC2,∴AC⊥CD
,∴AD2=AC2+DC2,∴AC⊥CD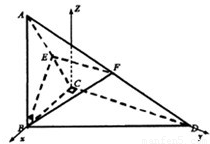
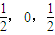 ),F(
),F( )
)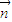 =(x,y,z),直线BD与平面BEF所成的角为θ
=(x,y,z),直线BD与平面BEF所成的角为θ =(
=( ),
),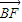 =(
=( )
)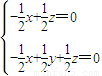 ,∴可取
,∴可取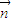 =(1,0,1)
=(1,0,1) =(-1,0,1)
=(-1,0,1) =
= =
= .
.
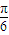


科目:高中数学 来源: 题型:
 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:
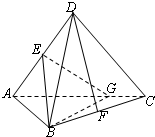 (2011•西安模拟)将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.
(2011•西安模拟)将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.查看答案和解析>>
科目:高中数学 来源:2014届吉林省长春市高一下学期期中理科数学试卷(解析版) 题型:填空题
如图所示,E、F分别是正方形SD1DD2的边D1D、DD2的中点沿SE,SF,EF将其折成一个几何体,使D1,D,D2重合,记作D。给出下列位置关系:①SD⊥面DEF; ②SE⊥面DEF; ③DF⊥SE; ④EF⊥面SED,其中成立的有
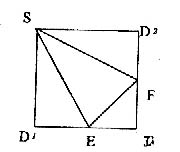
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
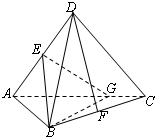 将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.
将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com