
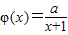 ,a为正常数.
,a为正常数.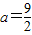 ,求函数f(x)的单调减区间;
,求函数f(x)的单调减区间;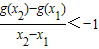 ,求a的取值范围.
,求a的取值范围.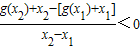 ,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.
,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.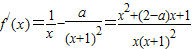 ,∵
,∵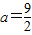 ,令f′(x)<0,
,令f′(x)<0, ,故函数f(x)的单调减区间为
,故函数f(x)的单调减区间为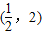 . …(5分)
. …(5分)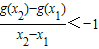 ,∴
,∴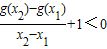 ,
, ,
,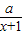 +x,
+x,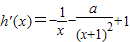 ,令h′(x)≤0,得a
,令h′(x)≤0,得a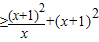 ═
═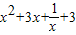 对x∈[1,2]恒成立
对x∈[1,2]恒成立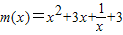 ,则
,则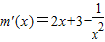 ,
,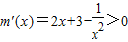 ,
,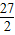 ,∴
,∴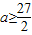 .
. ,
,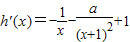 ,
,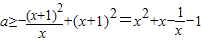 ,
,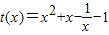 ,则
,则 ,∴t(x)在(0,1)上是增函数,
,∴t(x)在(0,1)上是增函数,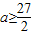 . …(16分)
. …(16分)

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2011年江苏省南京外国语学校高三考前适应性测试数学试卷(解析版) 题型:解答题
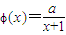 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;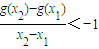 ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省天一中学、海门中学、盐城中学联考高三(下)2月调研数学试卷(解析版) 题型:解答题
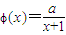 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;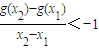 ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
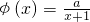 ,a为正常数.
,a为正常数.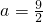 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;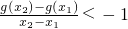 ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省福州市八县(市)一中高三(上)期中数学试卷(理科)(解析版) 题型:解答题
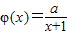 ,a为正常数.
,a为正常数.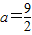 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;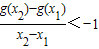 ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年江苏省扬州大学附中高考数学模拟试卷(解析版) 题型:解答题
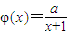 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间; ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com