
 已知四棱锥P-ABCD,底面ABCD为正方形,侧面PAD为直角三角形,且PA=PD,面PAD⊥面ABCD,E、F分别为AB、PD的中点.
已知四棱锥P-ABCD,底面ABCD为正方形,侧面PAD为直角三角形,且PA=PD,面PAD⊥面ABCD,E、F分别为AB、PD的中点.分析 (I)法1:取PC中点G,连接FG、BG,可得BE∥CD,又$BE=\frac{1}{2}DC$,可得BEFG为平行四边形,即证明EF∥BG,进而判定EF∥面PBC;法2:取CD中点H,连接FH,EH,通过证明平面EFH∥平面PBC,进而判定EF∥面PBC.
(II)利用线面垂直的性质可得CD⊥AP,进而证明PD⊥AP,即可证明线面垂直.
解答  (本小题满分12分)
(本小题满分12分)
证明:(I)法1:取PC中点G,连接FG、BG,-------------(1分)
因为F、G分别为PD、PC的中点,
所以FG∥CD且$FG=\frac{1}{2}DC$;-------------(2分)
因为ABCD为正方形,所以BE∥CD,
又因为E为AB中点,所以$BE=\frac{1}{2}DC$,
所以BE∥FG,且BE=FG,------(4分)
所以BEFG为平行四边形,所以EF∥BG;
因为EF?面PBC,BG?面PBC,
所以EF∥面PBC;-----------------------(6分)
法2:取CD中点H,连接FH,EH,-------------(1分)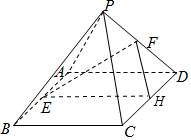
因为F,H分别为PD、CD的中点,
所以FH∥PC,EH∥BC;-------------(2分)
又FH?平面EFH,EH?平面EFH,PC?面PBC,BC?面PBC,
且FH∩EH=H,
所以平面EFH∥平面PBC,-----------------------(4分)
又因为EF?平面EFH,
所以EF∥面PBC;-----------------------(6分)
( II)因为ABCD为正方形,
所以CD⊥AD,---------------------(7分)
面PAD⊥面ABCD且AD为交线,
所以CD⊥面PAD,-----------------------(8分)
AP?面PAD,所以CD⊥AP,-----------------------(9分)
PAD为直角三角形,且PA=PD,
所以PD⊥AP,----------------------(10分)
又CD∩PD=D,
所以,AP⊥面PCD;-----------------------(12分)
点评 本题主要考查线面平行和线面垂直的判定,利用线面平行和线面垂直的判定定理是解决本题的关键,考查学生的空间想象能力和推理论证能力,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
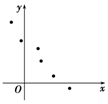
| A. | $\stackrel{∧}{y}$=1.5x+2 | B. | $\stackrel{∧}{y}$=-1.5x+2 | C. | $\stackrel{∧}{y}$=1.5x-2 | D. | $\stackrel{∧}{y}$=-1.5x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{3}{5}$ | C. | ∁UA∩∁UB | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com