
 ,
, ,
, ,
, ,
, ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题: 为合格产品的数量,求
为合格产品的数量,求 的分布列和数学期
的分布列和数学期 ;
; 
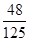
 为合格产品的数量,即可得求得相应的概率,从而根据数学期望的公式,求得结论.
为合格产品的数量,即可得求得相应的概率,从而根据数学期望的公式,求得结论. .
.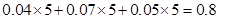 . 2 分
. 2 分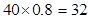 . 3 分
. 3 分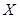 可能的取值为0,1,2, 4分
可能的取值为0,1,2, 4分 ,
,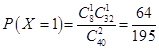 ,
,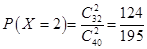 ,
,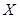 的分布列为
的分布列为 | 0 | 1 | 2 |
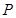 |  | 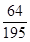 | 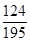 |
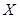 数学期望
数学期望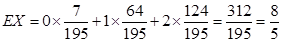 . 9分
. 9分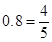 , 10分
, 10分 . 13分
. 13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
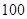 名年龄段在
名年龄段在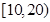 ,
,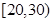 ,
,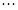 ,
,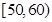 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.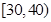 的人数;
的人数; 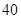 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取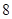 人,求
人,求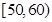 年龄段抽取的人数;
年龄段抽取的人数;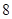 人中再抽取3人作为本次活动的获奖者,记
人中再抽取3人作为本次活动的获奖者,记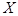 为年龄在
为年龄在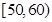 年龄段的人数,求
年龄段的人数,求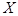 的分布列及数学期望.
的分布列及数学期望.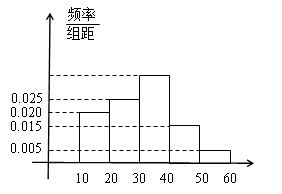
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
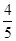 ,则每个学生补习的概率为( )
,则每个学生补习的概率为( )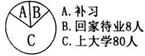
A.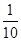 | B.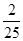 | C.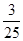 | D.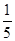 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4934 8200 3623 4869 6938 7481 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com