
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用导数判别函数的单调性求函数的最值可解决此问题;(2)利用导数判断函数的单调性可解决此问题.
(1)当k=-1时,![]() ,
,![]() =-exx-x=-x(ex+1)
=-exx-x=-x(ex+1)
当x<0时,![]() >0,当x>0时,
>0,当x>0时,![]() <0,所以f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,所以f(x)在x=0时取到最大值,最大值为f(0)=1.
<0,所以f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,所以f(x)在x=0时取到最大值,最大值为f(0)=1.
(2)![]() =kexx-x=x(kex-1),
=kexx-x=x(kex-1),
当k<0时,f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,又因为f(0)=-k>0,![]() ,
,![]() ,所以f(x)有两个零点;
,所以f(x)有两个零点;
当k=0时,![]() ,所以此时f(x)只有一个零点;
,所以此时f(x)只有一个零点;
当k=1时,![]() =exx-x=x(ex-1)≥0,f(x)在(-∞,+∞)上单调递增,f(x)不存在两个零点;
=exx-x=x(ex-1)≥0,f(x)在(-∞,+∞)上单调递增,f(x)不存在两个零点;
当0<k<1时,![]() ,f(x)在(-∞,0)上单调递增,在(0,-lnk)上单调递减,在(0,+∞)上单调递增,且f(0)=-k<0,f(x)不存在两个零点;
,f(x)在(-∞,0)上单调递增,在(0,-lnk)上单调递减,在(0,+∞)上单调递增,且f(0)=-k<0,f(x)不存在两个零点;
当k>1时,![]() ,f(x)在(-∞,-lnk)上单调递增,在(-lnk,0)上单调递减,在(0,+∞)上单调递增,且
,f(x)在(-∞,-lnk)上单调递增,在(-lnk,0)上单调递减,在(0,+∞)上单调递增,且![]() ,f(x)不存在两个零点.
,f(x)不存在两个零点.
综上,当f(x)有两个零点时,k的取值范围是(-∞,0).


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】某市疾控中心流感监测结果显示,自![]() 年
年![]() 月起,该市流感活动一度出现上升趋势,尤其是
月起,该市流感活动一度出现上升趋势,尤其是![]() 月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知
月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知![]() 位同学中有
位同学中有![]() 位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
方案乙:先任取![]() 个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这
个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这![]() 位中的
位中的![]() 位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外
位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外![]() 位同学中逐个检测;
位同学中逐个检测;
(1)求依方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)![]() 表示依方案甲所需化验次数,
表示依方案甲所需化验次数,![]() 表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6.
的周长为6.
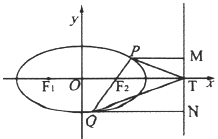
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 与
与![]() 轴的交点为
轴的交点为![]() .若四边形
.若四边形![]() 的面积是
的面积是![]() 面积的3倍,求直线
面积的3倍,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是梯形,AB∥DC,AD⊥DC,AB=AD=2,DC=3,平面PDC⊥平面ABCD,E在棱PC上且PE=2EC。
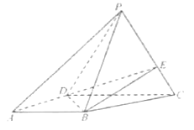
()证明:BE∥平面PAD;
(1)若ΔPDC是正三角形,求三棱锥P-DBE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是函数
是函数![]() 的导函数,且
的导函数,且![]() ,
,![]() ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①![]() ;
;
②曲线![]() 在
在![]() 处的切线斜率最小;
处的切线斜率最小;
③函数![]() 在
在![]() 存在极大值和极小值;
存在极大值和极小值;
④![]() 在区间
在区间![]() 上至少有一个零点.
上至少有一个零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com