
(1)求点(a,b)关于直线x+y=0的对称点的坐标;
(2)求点P(3,5)关于直线l∶x-3y+2=0的对称点的坐标;
(3)△ABC的顶点A(3,5),它的两条角平分线所在直线方程为x+y=0与x-3y+2=0,求BC边所在的直线方程.
|
(1) 设点(a,b)关于直线x+y=0的对称点为(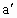 , ,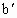 ),由 ),由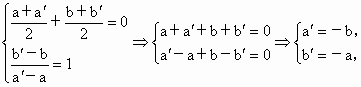
∴点 (a,b)关于直线x+y=0的对称点为(-b,-a).(2) 设P(3,5)关于直线l∶x-3y+2=0的对称称为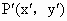 .直线PQ的斜率为 .直线PQ的斜率为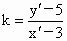 ,线段PQ的中点 ,线段PQ的中点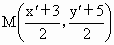 ,而直线l的斜率为 ,而直线l的斜率为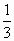 ,由PQ⊥l,且M在l上, ,由PQ⊥l,且M在l上,
得方程组 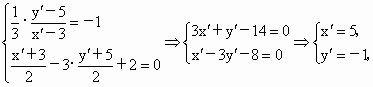
即点 Q的坐标为(5,-1).(3) ∵点A不在两条角平分线所在直线上,由(1)、(2)两小题结论,可知点A(3,5)关于x+y=0的对称点为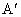 (-5,-3),关于x-3y+2=0的对称点为 (-5,-3),关于x-3y+2=0的对称点为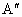 (5,-1).∵ (5,-1).∵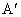 与 与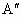 均在BC边所在直线上, 均在BC边所在直线上,
∴过 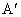 与 与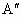 的直线方程为 的直线方程为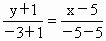 , ,
即 x-5y-10=0.∴ BC边所在直线方程为x-5y-10=0. |
|
(1)(2)利用两点关于直线对称的几何条件是两点连线与对称轴直线垂直,且两点连线的中点在对称轴直线上,然后布列方程组求解.(3)先要判断点A是否在两条角平分线上,再找出点A关于两角平分线的对称点,然后利用两点式求出BC边所在直线方程. 记住点 (a,b)关于x-y=0的对称点为(b,a);关于x+y=0的对称点为(-b,-a).当对称轴直线为x±y=0,x=a,y=b时,不必按(2)的解法去做,否则较为烦琐.同时应掌握一般情况下轴对称问题的解题方法. |


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:044
(1)
求点(a,b)关于直线x+y=0的对称点的坐标;(2)
求点P(3,5)关于直线l∶x-3y+2=0的对称点的坐标;(3)
△ABC的顶点A(3,5),它的两条角平分线所在直线方程为x+y=0与x-3y+2=0,求BC边所在的直线方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com