
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
(Ⅰ)由f(x)的图象经过P(0,2),知d=2,则
f(x)=x3+bx2+cx+2,f¢(x)=3x2+2bx+c,
由在M(-1,f(-1))处的切线方程是6x-y+7=0,知-6-f(-1)+7=0,即f(-1)=1,且f¢(-1)=6,
∴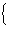
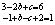 ,即
,即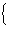
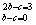 ,解得b=c=-3,
,解得b=c=-3,
故所求的解析式是f(x)=x3-3x2-3x+2.
(Ⅱ)f¢(x)=3x2-6x-3,令3x2-6x-3=0,即x2-2x-1=0,
解得x1=1-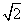 ,x2=1+
,x2=1+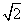 ,当x<1-
,当x<1-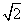 或x>1+
或x>1+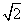 时,f¢(x)>0;
时,f¢(x)>0;
当1-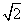 <x<1+
<x<1+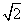 时,f¢(x)<0,
时,f¢(x)<0,
故f(x)=x3-3x2-3x+2在(-∞,1-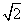 )内是增函数,在(1-
)内是增函数,在(1-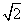 ,1+
,1+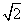 )内是减函数,在(1+
)内是减函数,在(1+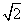 ,+∞)内是增函数.
,+∞)内是增函数.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
要得到函数y=3cosx的图象,只需将函数y=3sin(2x-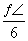 )的图象上所有点的( )
)的图象上所有点的( )
A.横坐标缩短到原来的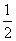 (纵坐标不变),所得图象再向左平移
(纵坐标不变),所得图象再向左平移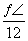 个单位长度
个单位长度
B.横坐标缩短到原来的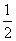 (纵坐标不变),所得图象再向右平移
(纵坐标不变),所得图象再向右平移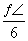 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移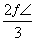 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移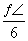 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
下列有关命题说法正确的是( )
A. 命题p:“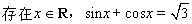 ”,则Øp是假命题
”,则Øp是假命题
B.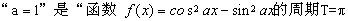 ”的充分必要条件
”的充分必要条件
C.命题 的否定是:“
的否定是:“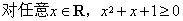 ”
”
D.命题“若tanα≠1,则α≠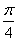 ” 的逆否命题是真命题
” 的逆否命题是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com