
【题目】如图,菱形ABCD中,AB=4,∠A=60°,以对角线BD为折痕把△ABD折起,使点A到达如图所示点E的位置,使![]() .
.
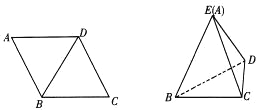
(1)求证:BD⊥EC;
(2)求三棱锥B-CE-D的余弦值.
【答案】(1)见解析;(2)二面角B-CE-D的余弦值为![]() .
.
【解析】
(1)根据菱形的对角线相互垂直,得到CO⊥BD且AO⊥BD,所以BD⊥平面EOC,从而得证;
(2)先证明OB,OC,OE三者两两垂直,以O为坐标原点.OB,OC,OE所在直线分别x、y、z轴建立空间直角坐标系O – xyz,求出平面BCE与平面CDE的法向量,代入公式即可得到结果.
(1)在图1中,连接A、C,设AC与BD相交于点O,由四边形ABCD为菱形可知![]() ,所以
,所以![]() ,由图2可知
,由图2可知
![]() ,
,
又![]() ,所以
,所以![]() 平面EOC,又
平面EOC,又![]() 平面EOC,所以
平面EOC,所以![]() .
.
(2)因为四边形ABCD为菱形且![]() ,所以
,所以![]() 为等边三角形
为等边三角形
又![]() ,所以
,所以![]() .所以
.所以![]() .
.
又![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() 平面BDC,所以OB,OC,OE三者两两垂直.
平面BDC,所以OB,OC,OE三者两两垂直.
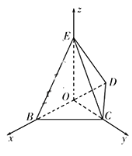
以O为坐标原点.OB,OC,OE所在直线分别x、y、z轴建立空间直角坐标系O – xyz,
则![]() ,
,
![]() .
.
设平面BCE的法向量为![]()
由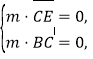 得
得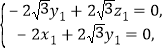 所以
所以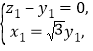
令![]() 得
得![]() ;
;
设平面CDE的法向量为![]() ,
,
由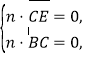 得
得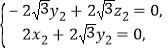 所以
所以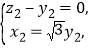 令
令![]() 得
得![]() ;故
;故![]() ,
,
由图可知二面角B-CE-D为锐角,所以二面角B-CE-D的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)如果存在过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与
与![]() 的倾斜角互补,求实数
的倾斜角互补,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为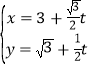 (
(![]() 为参数),点
为参数),点![]() 的极坐标为
的极坐标为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
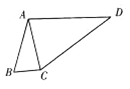
【题目】△ABC的内角A,B,C的对边分别为![]() ,已知
,已知![]() 且
且![]() .
.
(1)求角![]() ;
;
(2)如图,D为△ABC外一点,若在平面四边形ABCD中,![]() ,求△ACD面积的最大值.
,求△ACD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() 的部分图象如图所示,有下列结论:
的部分图象如图所示,有下列结论:
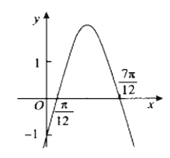
①函数![]() 的最小正周期为
的最小正周期为![]()
②函数![]() 在
在![]() 上的值域为
上的值域为![]()
③函数![]() 的一条对称轴是
的一条对称轴是![]()
④函数![]() 的图象关于点
的图象关于点![]() 对称
对称
⑤函数![]() 在
在![]() 上为减函数
上为减函数
其中正确的是______.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() (
(![]() ,
,![]() ).
).
(1)求函数![]() 的零点;
的零点;
(2)设![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() 为最简根式,若存在
为最简根式,若存在![]() ,使得
,使得![]() 可唯一表示为
可唯一表示为![]() 的形式(
的形式(![]() ),求证:
),求证:![]() ;
;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得![]()
成立,若存在,试求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com