

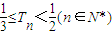 .
.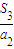 =
= 建立关于a1和q的方程,可解出q=2.从而得到数列{an}的首项a1=
建立关于a1和q的方程,可解出q=2.从而得到数列{an}的首项a1= ,得{an}的通项公式为an=a1qn-1=2n-2,由此结合题意和对数运算性质化简整理,可得bn=
,得{an}的通项公式为an=a1qn-1=2n-2,由此结合题意和对数运算性质化简整理,可得bn=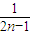 ;
;  (
(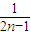 -
-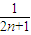 ),代入Tn消元化简得Tn=
),代入Tn消元化简得Tn= (1-
(1-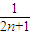 ),最后结合
),最后结合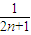 的取值范围,利用不等式的运算性质可证出不等式
的取值范围,利用不等式的运算性质可证出不等式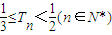 成立.
成立.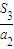 =
=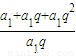 =
=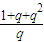 =
= ,
, )
) =
= ,得数列{an}的通项公式为an=a1qn-1=2n-2,
,得数列{an}的通项公式为an=a1qn-1=2n-2, =2得bn=
=2得bn=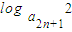 =
=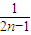 ;
; 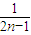 ;
; 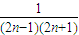 =
= (
( -
-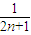 )
) [(1-
[(1- )+(
)+( -
-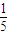 )+…+(
)+…+(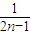 -
-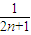 )]=
)]= (1-
(1-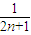 )
)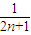 ≤
≤ ,得
,得 ≤1-
≤1-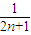 <1
<1 (1-
(1-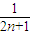 )∈[
)∈[ ,
, ),
), 成立.
成立.

科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源:温州一模 题型:单选题
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省温州市八校联考高三(上)9月月考数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com