Question

12．设函数f（x）=lnx-ax（a∈R）．
（1）若直线y=3x-1是函数f（x）图象的一条切线，求实数a的值；
（2）若函数f（x）在[1，e²]上的最大值为1-ae（e为自然对数的底数），求实数a的值；
（3）若关于x的方程ln（2x²-x-3t）+x²-x-t=ln（x-t）有且仅有唯一的实数根，求实数t的取值范围．

Answer 1

分析 （1）求出原函数的导函数，得到x=$\frac{1}{a+3}$，求出f（$\frac{1}{a+3}$）=ln$\frac{1}{a+3}$-$\frac{a}{a+3}$，代入直线y=3x-1求得a值；
（2）求出原函数的导函数，然后对a分类得到函数在[1，e²]上的单调性，并进一步求出函数在[1，e²]上的最大值，由最大值等于1-ae求得a值；
（3）把ln（2x²-x-3t）+x²-x-t=ln（x-t）转化为ln（2x²-x-3t）$+\frac{1}{2}$（2x²-x-3t）=ln（x-t）$+\frac{1}{2}$（x-t），构造函数g（x）=lnx+$\frac{1}{2}x$，则g（x）在（0，+∞）上是增函数，得到$\left\{\begin{array}{l}{t＜\frac{2{x}^{2}-x}{3}}\\{t＜x}\\{t={x}^{2}-x}\end{array}\right.$，画出图形，数形结合得答案．

解答 解：（1）由f（x）=lnx-ax，得f′（x）=$\frac{1}{x}-a$=3，
∴x=$\frac{1}{a+3}$，则f（$\frac{1}{a+3}$）=ln$\frac{1}{a+3}$-$\frac{a}{a+3}$，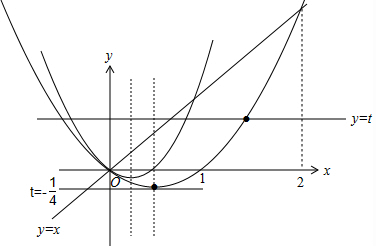
∴ln$\frac{1}{a+3}$-$\frac{a}{a+3}$=$\frac{3}{a+3}-1$，得ln$\frac{1}{a+3}$=0，即a=-2；
（2）f′（x）=$\frac{1}{x}-a$，
当a≤$\frac{1}{{e}^{2}}$时，f′（x）≥0在[1，e²]上恒成立，故f（x）在[1，e²]上为增函数，
故f（x）的最大值为f（e²）=2-ae²=1-ae，得$a=\frac{1}{{e}^{2}-e}$（舍）；
当$\frac{1}{{e}^{2}}$＜a＜1时，若x∈[1，$\frac{1}{a}$]，f′（x）＞0，x∈[$\frac{1}{a}，{e}^{2}$]，f′（x）＜0，
故f（x）在[1，e²]上先增后减，故$f（x）_{max}=f（\frac{1}{a}）=-lna-1$
由-lna-1=1-ae，解得a=$\frac{1}{e}$；
当a≥1时，故当x∈[1，e²]时，f′（x）≤0，f（x）是[1，e²]上的减函数，
故f（x）_max=f（1）=-a=1-ae，得a=$\frac{1}{e-1}$（舍）；
综上，a=$\frac{1}{e}$；
（3）ln（2x²-x-3t）+x²-x-t=ln（x-t）?ln（2x²-x-3t）$+\frac{1}{2}$（2x²-x-3t）=ln（x-t）$+\frac{1}{2}$（x-t），
令g（x）=lnx+$\frac{1}{2}x$，则g（x）在（0，+∞）上是增函数，
又g（2x²-x-3t）=g（x-t），
∴2x²-x-3t=x-t⇒2（x²-x-t）=0，
即$\left\{\begin{array}{l}{{x}^{2}-x-t=0有唯一实根}\\{x-t＞0}\\{2{x}^{2}-x-3t＞0}\end{array}\right.$⇒$\left\{\begin{array}{l}{t＜\frac{2{x}^{2}-x}{3}}\\{t＜x}\\{t={x}^{2}-x}\end{array}\right.$，
作出图象如图：由图可知，实数t的取值范围是t=-$\frac{1}{4}$或0≤t＜2．

点评 本题考查利用导数研究函数的单调性考查了利用导数求函数的最值，考查数学转化、分类讨论、数形结合等数学思想方法，难度较大．