分析:(1)由题意取A1B1中点M,再证明C1M⊥平面A1ABB1,即∠C1BM是所求的角,在Rt△BMC1中求解;
(2)取A1C1的中点D1,AC1的中点F,再证D1FEB1是平行四边形和B1D1⊥平面ACC1A1,即得EF⊥平面ACC1A1,故证出面面垂直;
(3)由(2)知EF是三棱锥E-ACC1的高,求出EF的长,再利用换低公式和体积相等求出点C1到平面AEC的距离.
解答:(1)解:取A
1B
1中点M,连接C
1M,BM.
∵三棱柱ABC-A
1B
1C
1是正三棱柱,
∴C
1M⊥A
1B
1,C
1M⊥BB
1.
∴C
1M⊥平面A
1ABB
1.
∴∠C
1BM为直线C
1B与平面A
1ABB
1所成的角.
在Rt△BMC
1中,C
1M=
a,BC
1=
a,
∴sin∠C
1BM=
=
.
(2)证明:取A
1C
1的中点D
1,AC
1的中点F,连接B
1D
1、EF、D
1F.
则有D
1F
AA
1,B
1E
AA
1.
∴D
1F
B
1E.
则四边形D
1FEB
1是平行四边形,
∴EF
B
1D
1.
由于三棱柱ABC-A
1B
1C
1是正三棱柱,
∴B
1D
1⊥A
1C
1.
又∵平面A
1B
1C
1⊥平面ACC
1A
1于A
1C
1,且B
1D
1?平面A
1B
1C
1,
∴B
1D
1⊥平面ACC
1A
1,∴EF⊥平面ACC
1A
1.
∵EF?平面AEC
1,∴平面AEC
1⊥平面ACC
1A
1.
(3)由(2)知,EF⊥平面AC
1,则EF是三棱锥E-ACC
1的高.
由三棱柱各棱长都等于a,则EC=AE=EC
1=
a,AC
1=
a.
∴EF=
=
a.
∵V
_C1-AEC=V
_E-ACC1,设三棱锥V
_C1-AEC的高为h,则h为点C
1到平面AEC的距离.
则
S
△AEC•h=
S
_△ACC1•EF,
即
×
a
2h=
×
a
2•
a.
∴h=
a,即点C
1到平面AEC的距离是
a.
点评:本题考查了用面面垂直的性质定理作出线面角再来求解,用面面垂直的判定定理证明面面垂直,求点到面的距离可用体积相等和换底求解;考查了转化思想和推理论证能力.

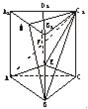
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.


 (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.