
设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,(
,(![]() )
)
其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() ≤
≤![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
解: (1)依题意,知![]() 的定义域为(0,+∞),
的定义域为(0,+∞),
当![]() 时,
时,![]() ,
,
![]() ……………3分
……………3分
令![]() =0,解得
=0,解得![]() .(∵
.(∵![]() )
)
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减。
单调递减。
所以![]() 的极大值为
的极大值为![]() ,此即为最大值 ……………5分
,此即为最大值 ……………5分
(2)![]() ,
,![]() ,则有
,则有![]() ≤
≤![]() ,在
,在![]() 上恒成立,所以
上恒成立,所以![]() ≥
≥![]() ,
,![]()
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ≥
≥![]() ………9分
………9分
(3)因为方程![]() 有唯一实数解,
有唯一实数解,
所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,
,
则![]() .令
.令![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在(0,
在(0,![]() )上单调递减,
)上单调递减,
当![]() 时,
时,![]() ,
,![]() 在(
在(![]() ,+∞)单调递增
,+∞)单调递增
当![]() 时,
时,![]() =0,
=0,![]() 取最小值
取最小值![]() .
.
则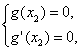 即
即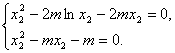 ……………11分
……………11分
所以![]() ,因为
,因为![]() ,所以
,所以![]() (*)
(*)
设函数![]() ,因为当
,因为当![]() 时,
时,
![]() 是增函数,所以
是增函数,所以![]() 至多有一解.
至多有一解.
因为![]() ,所以方程(*)的解为
,所以方程(*)的解为![]() ,即
,即![]() ,
,
解得![]() ……………14分
……………14分


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源:黑龙江龙东地区2011-2012学年高二上学期高中教学联合体期末考试数学文科试题 题型:044
设函数![]()
(1)当![]() 曲线
曲线![]() 处的切线方程
处的切线方程
(2)求函数的单调区间与极值;
(3)已知函数f(x)有三个互不相同的零点0,x1,x2,且x1<x2.若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012高三数学一轮复习单元练习题 函数与数列(1) 题型:044
设函数![]()
(1)当m=1时,曲线y=f(x)在点(1,f(1))处的切线斜率
(2)求函数的单调区间与极值;
(3)已知函数f(x)有三个互不相同的零点0,x1,x2,且x1<x2.若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年西藏拉萨中学高三第5次月考数学文卷 题型:解答题
、已知函数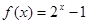 的反函数为
的反函数为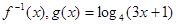
(1)若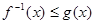 ,求
,求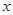 的取值范围D;
的取值范围D;
(2)设函数 ;当
;当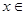 D时,求函数H
D时,求函数H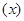 的值域
的值域
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com