解:(I)证明:令y=x,则f(4x)=4f(x)
令x=y=0,则f(0)=0
令y=0,则f(3x)=3f(x)
(II)解:f(x)在(-∞,+∞)上是减函数,以下证明:
任设x
1,x
2∈(-∞,+∞),且x
1>x
2,则
f(x
1)-f(x
2)=f(
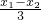
×3+x
2)-f(x
2)=3f(
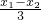
)
∵x
1-x
2>0
∴f(
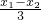
)<0
即f(x
1)-f(x
2)<0,即f(x
1)<f(x
2)
∴f(x)在(-∞,+∞)上是减函数
(III)解:∵f(8)=-2
∴4f(2)=2,∴f(2)=-

12f(log
2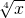
)=3f(4log
2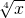
)=3f(log
2x)
∴

=
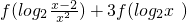
=
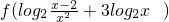
=f(log
2[x(x-2)])
∴
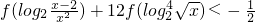
?f(log
2[x(x-2)])<f(2)
?
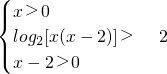
?
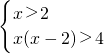
?
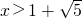
∴不等式的解集为
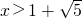
分析:(I)使用赋值法,先令y=x,得f(4x)=4f(x),再令x=y=0,得f(0)=0,最后令y=0,得f(3x)=3f(x)
(II)利用函数单调性的定义以及已知抽象表达式,x>0时,f(x)<0.即可证明f(x)在(-∞,+∞)上是减函数
(III)先利用抽象表达式得f(2)=-

,再利用对数运算性质及函数的单调性,将不等式转化为对数不等式组,解之即可
点评:本题综合考查了抽象表达式的意义和作用,函数单调性的定义及证明,利用函数的单调性解不等式的技巧

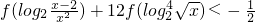 .
.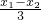 ×3+x2)-f(x2)=3f(
×3+x2)-f(x2)=3f(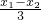 )
)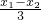 )<0
)<0
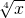 )=3f(4log2
)=3f(4log2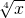 )=3f(log2x)
)=3f(log2x) =
=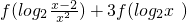
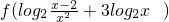 =f(log2[x(x-2)])
=f(log2[x(x-2)])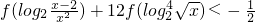 ?f(log2[x(x-2)])<f(2)
?f(log2[x(x-2)])<f(2)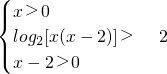 ?
?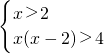 ?
?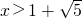
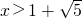
 ,再利用对数运算性质及函数的单调性,将不等式转化为对数不等式组,解之即可
,再利用对数运算性质及函数的单调性,将不等式转化为对数不等式组,解之即可

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案