
已知关于x的不等式1+2x+(a-a2)4x<0在[0,+∞)上恒成立,求实数a的取值范围(提示:a2-a-2>0![]() a<-1,或a>2).
a<-1,或a>2).
分析:将不等式中的未知数x与参数a分别移到不等式的两边,即将原不等式转化为g(a)<f(x)的形式,再利用g(a)<f(x)min求解.
解:由于4x>0,故可将原不等式转化为
a-a2<-![]() -
-![]() =-
=-![]() -
-![]() ,
,
则该不等式在[0,+∞)上恒成立.
设y=f(x)=-![]() -
-![]() ,
,
令u(x)=![]() >0,y=-u2-u=-
>0,y=-u2-u=-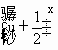 +
+![]() ,
,
因为0<![]() <1,且-
<1,且-![]() <0,
<0,
所以u(x)在R上为减函数,y=-u2-u在(0,+∞)上为减函数,
所以函数f(x)在[0,+∞)上为增函数,
所以f(0)≤f(x),即-2≤f(x),
所以a-a2<-2,即a2-a-2>0,解得a<-1,或a>2.
所以,实数a的取值范围是(-∞,-1)∪(2,+∞).
点评:利用指、对数函数的单调性求解不等式的恒成立问题,主要有两种方法:(1)分离参数法,即将不等式中的参数分离出来,使不等式的一端化为只含参数的解析式,而另一端化为含未知数的解析式,再利用单调性解答,整个过程体现函数思想;(2)利用指、对数函数的单调性将不等式转化为一般的代数不等式,再结合其他方法,如判别式法、图象法等来求解.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕头市潮阳实验学校高三(上)第二周周练数学试卷(理科)(解析版) 题型:解答题
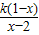 +1<0的解集为空集,求实数k的取值或取值范围.
+1<0的解集为空集,求实数k的取值或取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com