
已知轴对称平面五边形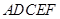 (如图1),
(如图1),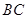 为对称轴,
为对称轴,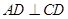 ,
,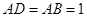 ,
,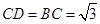 ,将此图形沿
,将此图形沿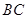 折叠成直二面角,连接
折叠成直二面角,连接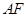 、
、 得到几何体(如图2).
得到几何体(如图2).

(Ⅰ)证明: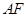 ∥平面
∥平面 ;
;
(Ⅱ)求二面角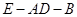 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:解答题
已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ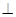 BQ并说明理由.
BQ并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图(1),在等腰直角三角形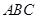 中,
中,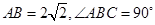 ,点
,点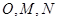 分别为线段
分别为线段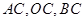 的中点,将
的中点,将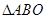 和
和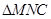 分别沿
分别沿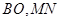 折起,使二面角
折起,使二面角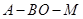 和二面角
和二面角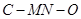 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。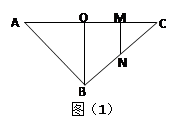

(1)求证: 面
面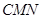 ;
;
(2)求平面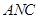 与平面
与平面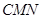 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)求点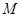 到平面
到平面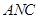 的距离。
的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com