
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 函数f(x),g(x)满足$\int_{-2}^2$f(x)g(x)=0,则y=f(x)g(x)为奇函数,判断被积函数的奇偶性即可得出结论.
解答 解:函数f(x),g(x)满足$\int_{-2}^2$f(x)g(x)=0,则y=f(x)g(x)为奇函数,
对于①:f(x)=sinx,g(x)=cosx,∴y=sinx•cosx为奇函数,∴f(x),g(x)为区间[-2,2]上的一组正交函数;
对于②:f(x)=x2+1,g(x)=x2-1,y=(x2+1)(x2-1)偶函数,∴f(x),g(x)不是区间[-2,2]上的一组正交函数;
对于③:f(x)=ex,g(x)=ex+1,∴y=ex(ex+1),为非奇非偶函数,∴f(x),g(x)不是区间[-2,2]上的一组正交函数
对于④:f(x)=$\frac{1}{2}$x,g(x)=x2,∴y=$\frac{1}{2}$x3,为奇函数,∴f(x),g(x)为区间[-2,2]上的一组正交函数,
∴正交函数有2组,
故选:B.
点评 本题考查新定义,考查微积分基本定理的运用,属于基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在一标准大气压下,20℃的纯水结冰 | |
| B. | 平时的百分制考试中,小白的考试成绩为100分 | |
| C. | 抛一枚硬币,落下后正面朝上 | |
| D. | 边长为a,b的长方形面积为ab |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
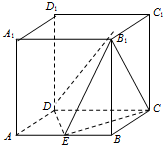 如图,在正方体ABCD-A1B1C1D1中,E为AB上一点.
如图,在正方体ABCD-A1B1C1D1中,E为AB上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com