(12分)设函数f(x)＝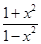
.
(1)求f(x)的定义域；(2)判断f(x)的奇偶性；(3)求证：f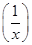
＋f(x)＝0.
） (1)函数f(x)的定义域为{x∈R|x≠±1}．(2) f(x)为偶函数．(3)证明：见解析。
【解析】本试题主要是考查了函数的定义域和奇偶性的判定以及函数解析式的运用
（1）因为由解析式知，函数应满足1－x2≠0，即x≠±1.
∴函数f(x)的定义域为{x∈R|x≠±1}．
（2）由(1)知定义域关于原点对称，
f(－x)＝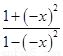
＝
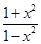＝f(x)
（（3）根据解析式求解f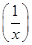
＋f(x)＝0.即可得证。
解：(1)由解析式知，函数应满足1－x2≠0，即x≠±1.
∴函数f(x)的定义域为{x∈R|x≠±1}．
(2)由(1)知定义域关于原点对称，
f(－x)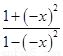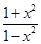＝＝＝f(x)．
∴f(x)为偶函数．
(3)证明：∵f＝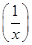
＝
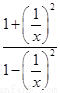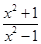，f(x)＝，
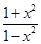∴f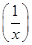＋f(x)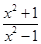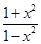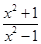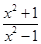＝＋＝－＝0.
名校课堂系列答案科目：高中数学 来源： 题型：
查看答案和解析>>
科目：高中数学 来源：2011年辽宁省招生统一考试文科数学 题型：解答题
（本小题满分12分）
设函数f（x）=x+ax2+blnx，曲线y=f（x）过P（1,0），且在P点处的切斜线率为2.
（I）求a，b的值；
（II）证明：f(x)≤2x-2。
查看答案和解析>>
科目：高中数学 来源：2010-2011学年河南省许昌市四校高三第一次联考数学卷 题型：解答题
（本小题满分12分）设函数f（x）=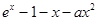
（1）若a=0，求f（x）的单调区间；
（2）若当x≥0时f（x）≥0，求a的取值范围
查看答案和解析>>
科目：高中数学 来源：2010-2011学年宁夏高三第一次模拟考试数学文卷 题型：解答题
（本小题满分12分）
设函数f(x)=lnx，g(x)=ax+
，函数f(x)的图像与x轴的交点也在函数g(x)的图像上，且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值；
(Ⅱ) 设x>0，试比较f(x)与g(x)的大小.
查看答案和解析>>
科目：高中数学 来源：2010年河南省辉县市高二上学期第二次阶段性考试数学卷 题型：解答题
（本小题满分12分）设函数f(x)＝m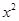
－mx－1.
（1）若对于一切实数x，f(x)<0恒成立，求m的取值范围；
（2）对于x∈[1,3]，f(x)<0恒成立，求m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com