
 倍,
倍,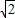 倍,
倍,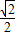 倍,
倍, 个单位,⑧向右平移
个单位,⑧向右平移 个单位,
个单位, 个单位,⑩向右平移
个单位,⑩向右平移 个单位,
个单位,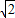 sin(2x+
sin(2x+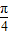 )-1,由三角函数的周期公式可算出最小正周期为T=π,结合三角函数图象变换的方法,可得y=sin2x的图象按照⑨③⑥或③⑨⑥的顺序变换,可得y=f(x)的图象;
)-1,由三角函数的周期公式可算出最小正周期为T=π,结合三角函数图象变换的方法,可得y=sin2x的图象按照⑨③⑥或③⑨⑥的顺序变换,可得y=f(x)的图象;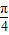 ,代入三角形面积公式算出c=3
,代入三角形面积公式算出c=3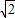 ,最后利用余弦定理即可算出边a的长.
,最后利用余弦定理即可算出边a的长.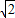 sin(2x+
sin(2x+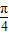 )-1…(3分)
)-1…(3分)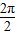 =π …(5分)
=π …(5分)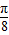 ,然后横坐标不变、纵坐标变为原来
,然后横坐标不变、纵坐标变为原来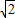 倍,
倍,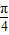 )=
)=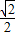 ,且2A+
,且2A+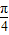 ∈(
∈( ,
,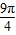 )
)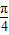 =
=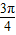 ,解之得A=
,解之得A=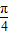 …(10分)
…(10分) bcsinA=
bcsinA= ×4×csin
×4×csin =6,解之得c=3
=6,解之得c=3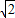 …(10分)
…(10分)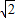 cos
cos =10
=10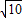 (舍负)…(14分).
(舍负)…(14分).

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源:2013年河北省石家庄一中高考数学一模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2012年河北省石家庄市高考数学一模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com