
((本题15分)
已知函数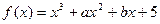 ,
,
(Ⅰ)若曲线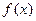 在点
在点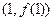 处的切线斜率为3,且
处的切线斜率为3,且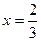 时
时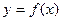 有极值,求函数
有极值,求函数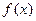 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,求函数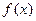 在
在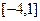 上的最大值和最小值。
上的最大值和最小值。
解:
科目:高中数学
来源:
题型:
(本题15分) 已知椭圆 (Ⅰ)求椭圆的方程; (Ⅱ)若 (Ⅲ)若坐标原点
科目:高中数学
来源:2011届浙江省瑞安中学高三上学期10月月考文科数学卷
题型:解答题
(本题15分)
科目:高中数学
来源:2012-2013学年浙江省高三回头考联考理科数学试卷(解析版)
题型:解答题
(本题15分)已知点 (Ⅰ)求椭圆E的方程; (Ⅱ)设A、B是椭圆E上两个动点, (Ⅲ)在(Ⅱ)的条件下,当△PAB面积取得最大值时,求λ的值.
科目:高中数学
来源:2010-2011学年浙江省高三上学期10月月考文科数学卷
题型:解答题
(本题15分) 已知抛物线 (1)用 (2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区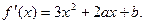 (2分)
(2分)
(Ⅰ)由题意,得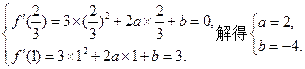 (6分)
(6分)
所以,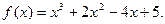 …………………………………………7分
…………………………………………7分
(Ⅱ)由(Ⅰ)知,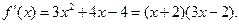 ,
,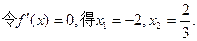 (9分)
(9分)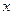
-4 (-4,-2)  -2
-2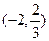
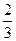
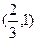
1 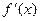
+ 0 - 0 + 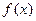

极大值 
极小值 
函数值 -11 解析


七彩口算题卡系列答案
自我提升与评价系列答案
一课一卷随堂检测系列答案
壹学教育计算天天练系列答案
基础训练济南出版社系列答案
全效学习学案导学设计系列答案
课堂伴侣课程标准单元测评系列答案
名师大课堂同步核心练习系列答案
初中暑假作业南京大学出版社系列答案
长江作业本实验报告系列答案
![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,
,![]() .
.![]() ,且
,且![]() ,求
,求![]() 的值(
的值(![]() 点为坐标原点);
点为坐标原点);![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
已知抛物线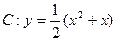 ,点
,点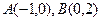 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设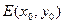 ,C,D在直线AB上,
,C,D在直线AB上,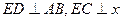 轴。
轴。
(1)用 表示
表示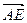 在
在 方向上的投影;
方向上的投影;
(2)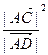 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。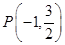 是椭圆E:
是椭圆E: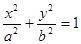 (
(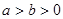 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.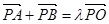 (
(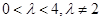 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;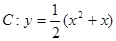 ,点
,点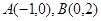 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设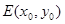 ,C,D在直线AB上,
,C,D在直线AB上,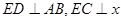 轴。
轴。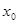 表示
表示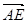 在
在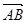 方向上的投影;
方向上的投影;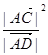 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号