
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:选择题
已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为 ,
,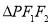 是以
是以 为底边的等腰三角形,若
为底边的等腰三角形,若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽合肥一中高二上月考一数学(文)试卷(解析版) 题型:填空题
如图所示,在直三棱柱 中,底面为直角三角形,
中,底面为直角三角形, 是
是 上一动点,则
上一动点,则 的最小值是______________.
的最小值是______________.

查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽合肥一中高二上月考一数学(文)试卷(解析版) 题型:选择题
如图,在棱长为2的正方体 中,
中, 是底面
是底面 的中心,
的中心, 分别是
分别是 的中点,那么异面直线
的中点,那么异面直线 与
与 所成角的余弦值等于( )
所成角的余弦值等于( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017年福建福州外国语学校高二文上月考一数学试卷(解析版) 题型:解答题
围建一个面积为 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为 元/
元/ ,新墙的造价为
,新墙的造价为 元/
元/ ,设利用的旧墙的长度为
,设利用的旧墙的长度为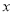 ,费用为
,费用为 元.
元.

(1)将 表示为
表示为 的函数;
的函数;
(2)试确定 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源:2016-2017年福建福州外国语学校高二理上月考一数学试卷(解析版) 题型:解答题
某小型餐馆一天中要购买 ,
, 两种蔬菜,
两种蔬菜, ,
, 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要 蔬菜至少要买6公斤,
蔬菜至少要买6公斤, 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出, ,
, 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
查看答案和解析>>
科目:高中数学 来源:2017届河北唐山市高三上学期调研统考一数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
坐标原点为极点, 轴的正半轴为极轴建立极坐标系.曲线
轴的正半轴为极轴建立极坐标系.曲线 的极坐标方程是
的极坐标方程是 .矩形
.矩形 内接于曲线
内接于曲线 ,
, 两点的极坐标分别为
两点的极坐标分别为 和
和 .将曲线
.将曲线 上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线
上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线 .
.
(1)写出 的直角坐标及曲线
的直角坐标及曲线 的参数方程;
的参数方程;
(2)设 为
为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com