
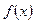 的定义域为
的定义域为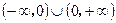 ,且满足条件:①
,且满足条件:① ,②
,② ③当
③当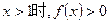 .
.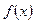 为偶函数;
为偶函数;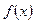 的单调性;
的单调性;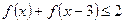 的解集
的解集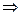 f(1)=0,
f(1)=0, )+ f(-1)
)+ f(-1)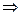 f(-1)=0,
f(-1)=0,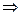 f(x), ∴f(x)为偶函 数;
f(x), ∴f(x)为偶函 数;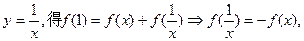
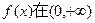 上的单调性, 任取x1http:///x2,设x2>x1>0,
上的单调性, 任取x1http:///x2,设x2>x1>0,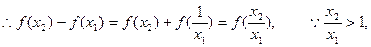
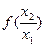 >0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数,
>0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数, 4)= f(-4),
4)= f(-4), 增函数,
增函数,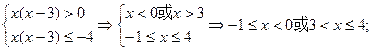
 , ∵f(x)在(-∞,0)上为减函数;
, ∵f(x)在(-∞,0)上为减函数;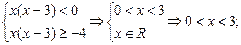

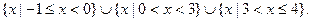


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com