
 )第一题满分5分,第二题满分5分,第三题满分8分.
)第一题满分5分,第二题满分5分,第三题满分8分. 条交线ED,CB, E1 D1的关系。
条交线ED,CB, E1 D1的关系。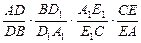 的值;
的值;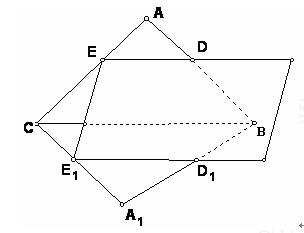
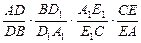 的值变化吗?为什么?
的值变化吗?为什么?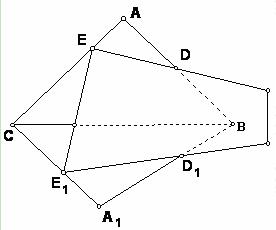
 平面DEE1D1=ED
平面DEE1D1=ED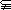 平面DEE1D1 ∴H∈平面DEE1D1
平面DEE1D1 ∴H∈平面DEE1D1 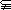 平面ABC,平面ABC∩平面DEE1D1="ED "
平面ABC,平面ABC∩平面DEE1D1="ED " 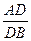 =
=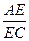 同理可得
同理可得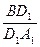 =
=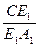
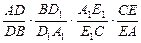 =
=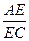
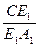
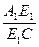
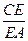 =1
=1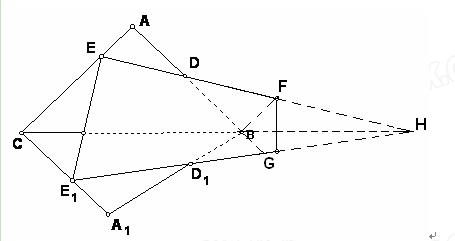
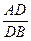 =
=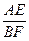
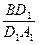 =
=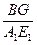
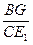 =
=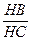
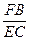 =
=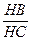
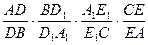 =
=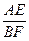
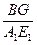
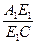
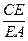 =
=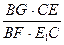 =
=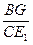
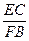 =
=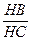
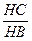 =1
=1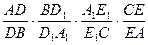 的值不变化,仍为1
的值不变化,仍为1

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
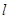 、
、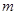 ,平面
,平面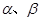 ,则下列命题中:
,则下列命题中:  ,
,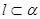 ,则
,则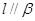
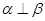 ,
,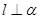 ,则
,则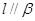
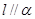 ,
,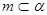 ,则
,则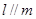
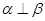 ,
,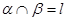 ,
, 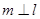 ,则
,则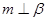 ,其中真命题有( )
,其中真命题有( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中,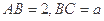 ,又
,又 ⊥平面
⊥平面 ,
,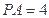 .
.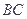 上存在一点
上存在一点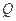 ,使
,使 ,
,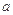 的取值范围;
的取值范围;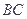 上存在唯一点
上存在唯一点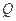 ,使
,使 时,
时,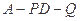 的余弦值.
的余弦值.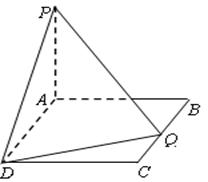
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
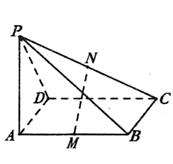
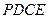 为矩形,四边形
为矩形,四边形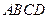 为梯形,平面
为梯形,平面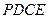
 平面
平面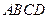 ,
,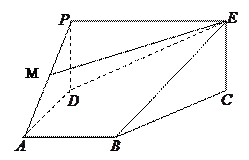
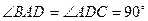 ,
,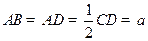 ,
, .
. (Ⅰ)若
(Ⅰ)若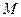 为
为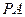 中点,求证:
中点,求证: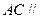 平面
平面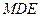 ;
;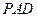 与
与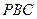 所成锐二面角的大小.
所成锐二面角的大小. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com