
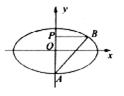
如图所示,点A是椭圆C:![]() 的短轴位于
的短轴位于![]() 轴下方的端点,过A作斜率为1的直线交椭圆于B点,点P在
轴下方的端点,过A作斜率为1的直线交椭圆于B点,点P在![]() 轴上,且BP//
轴上,且BP//![]() 轴,
轴,![]() ;
;
(1)若点P的坐标为(0,1),求椭圆C的方程;
(2)若点P的坐标为(0,![]() ),求实数
),求实数![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 给出下列5个命题:
给出下列5个命题:| 1 |
| 5 |
| 1 |
| 1-a |
| 2a |
tan2x+
| ||
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:吉林省长春市十一高2011-2012学年高二下学期期中考试数学理科试题 题型:013
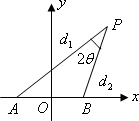
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2![]() ,且存在常数λ(0<λ<1),使得
,且存在常数λ(0<λ<1),使得![]() .(如图所示)那么点P的轨迹是
.(如图所示)那么点P的轨迹是
A.圆
B.椭圆
C.双曲线
D.抛物线
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
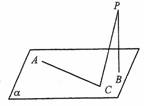
(08年北师大附中月考文) 如图所示,定点A和B都在平面α内,定点P![]() α,PB⊥α,C是α内异于A和B的动点,且PC⊥AC,那么,动点C在平面α内的轨迹是( )
α,PB⊥α,C是α内异于A和B的动点,且PC⊥AC,那么,动点C在平面α内的轨迹是( )
A.一条线段,但要去掉两个点
B.一个圆,但要去掉两个点
C.一个椭圆,但要去掉两个点
D.半圆,但要去掉两个点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com