
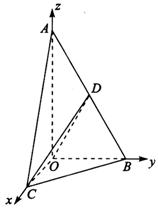
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当D为AB的中点时,求异面直线AO与CD所成角的大小;
(Ⅲ)求CD与平面AOB所成角的最大值.
解法一:
(Ⅰ)由题意,CO⊥AO,BO⊥AO,
∴∠BOC是二面角B-AO-C的平面角.
又∵二面角B-AO-C是直二面角,
∴CO⊥BO,又∵AO∩BO=O,
∴CO⊥平面AOB,
又CO![]() 平面COD,
平面COD,
∴平面COD⊥平面AOB.
(Ⅱ)作DE⊥OB,垂足为E,连结CE(如图),则DE∥AO,
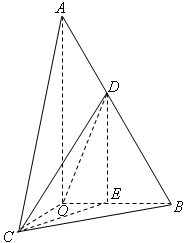
∴∠CDE是异面直线AO与CD所成的角.
在Rt△COE中,CO=BO=2,OE=![]() BO=1,
BO=1,
∴CE=![]() .
.
又DE=![]() AO=
AO=![]() ,
,
∴在Rt△CDE中,tan∠CDE=![]() ,
,
∴异面直线AO与CD所成角的大小为arctan![]() .
.
(Ⅲ)由(Ⅰ)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角,且tan∠CDO=![]() .
.
当OD最小时,∠CDO最大,
这时,OD⊥AB,垂足为D,OD=![]() =
=![]() ,tan∠CDO=
,tan∠CDO=![]() ,
,
∴CD与平面AOB所成角的最大值为arctan![]() .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ)建立空间直角坐标系O-xyz,如图,
则O(0,0,0),A(0,0,2![]() ),C(2,0,0),D(0,1,
),C(2,0,0),D(0,1,![]() ),
),
∴![]() =(0,0,2
=(0,0,2![]() ),
),![]() =(-2,1,
=(-2,1,![]() ),
),
∴cos〈![]() ,
,![]() 〉=
〉=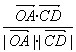 =
=![]() ,
,
∴异面直线AO与CD所成角的大小为arccos![]() .
.

(Ⅲ)同解法一


科目:高中数学 来源: 题型:
| 3 |
| 3 |
 ,当点P在⊙F1上运动时M形成曲线C.(如图)
,当点P在⊙F1上运动时M形成曲线C.(如图)| 3 |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.4 B![]() D.
D.![]()

图
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分) 矩形ABCD中,AB =2,AD = ,H是AB中点,以H为直角顶点作矩形的内接直角三角形HEF,其中E,F分别落在线段BC和线段AD上,如图.记∠BHE为θ,记Rt△EHF的周长为 l.⑴试将 l 表示为 θ 的函数;
⑵求 l 的最小值及此时的 θ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com