
| PA |
| PB |
| PC |
| O |
| BA |
| PD |
| PE |
| 1 |
| 3 |
| BA |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
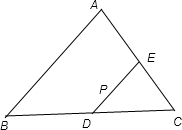 解:如图:设D、E 分别为BC、AC的中点,
解:如图:设D、E 分别为BC、AC的中点,| PA |
| PB |
| PC |
| PA |
| PB |
| PB |
| PC |
| BA |
| PD |
| PD |
| PA |
| PC |
| PB |
| PC |
| PE |
| PD |
| PE |
| 1 |
| 3 |
| BA |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古包头33中高一(下)期末数学试卷(理科)(解析版) 题型:填空题
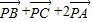 =
=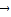 ,现随机将一颗豆子撒在△ABC内,则豆子落在△PBC内的概率为 .
,现随机将一颗豆子撒在△ABC内,则豆子落在△PBC内的概率为 .查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省宝鸡中学高三(上)第一次月考数学试卷(理科)(解析版) 题型:选择题
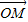 =
=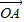 +λ(
+λ(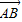 +
+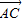 ),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )
),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com