
分析 (1)利用构造法将函数进行转化,结合等比数列的定义进行证明.
(2)根据bn=an+1的关系即可求出数列{an}的通项公式an,利用等比数列的前n项和公式以及分组法进行求解即可.
解答 证明:(1)∵an+1=3an+2,
∴1+an+1=3an+2+1=3(an+1),
∵a1=2,bn=an+1
∴bn+1=3bn,
即$\frac{{b}_{n+1}}{{b}_{n}}$=3,则数列{bn}是公比q=3的等比数列.
(2)∵数列{bn}是公比q=3的等比数列,首项b1=a1+1=2+1=3,
则bn=3•3n-1=3n=an+1,
则an=3n-1.
则Sn=$\frac{3(3-{3}^{n})}{1-3}$-n=$\frac{3}{2}$(3n-1)-n.
点评 本题主要考查数列通项公式和前n项和公式的计算,根据条件利用构造法结合等比数列的定义是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
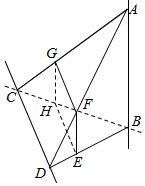 如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.
如图所示,异面直线AB,CD互相垂直,AB=$\sqrt{6}$,BC=$\sqrt{3}$,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
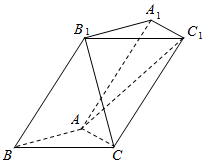 如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.
如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
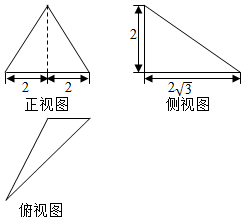
| A. | 4$\sqrt{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | 8$\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,1)∪(2,+∞) | C. | (-∞,0)∪(0,2) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | “?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0” | |
| C. | 命题“若a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” | |
| D. | 若命题“¬p”与“p或q”都是真命题,则命题q一定是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com