练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下表是我国居民生活污水排放量的一组数据：

    年份

    1997

    1998

    1999

    2000

    2001

    2002

    2003

    2004

    排放量

    151

     

    189.1

    194.8

    203.8

    220.9

    227.7

    232.3

    试估计1998年我国居民生活污水排放量，并预测2006年生活污水排放量.(单位：102t)

    思路分析：本题考查要估计或预测，可先考虑求线性回归直线方程.将年份与污水排放量的相关关系表达出来，可先剔除1998年，样本容量为7.

    解：设年份为x，污水排放量为y,则样本容量为7，分别求出x，y，，，，代入公式可求得回归直线方程.

    从而求得1998年的估计及2006年的预测值.

        巧解提示 上述方法看上去很合理，但运算量太大，本题只是利用回归方程预测估计，可以将变量作适当调整，以体现出变量的取值及两变量的变化趋势相关关系.

    另解：以1997年为第1年，…，2004年为第8年.列表，用科学计算器进行有关计算：

    i

    1

    2

    3

    4

    5

    6

    7

    xi

    1

    3

    4

    5

    6

    7

    8

    yi

    151

    189.1

    194.8

    203.8

    220.9

    227.7

    232.3

    xiyi

    151

    567.3

    779.2

    1 019

    1 325.4

    1 593.9

    1 858.4

    =4.857,=202.8,=200,=292 648.68,=7 294.2

    所以b==14.368.

    a=-b=202.8-14.368×4.857=133.058.

    回归直线方程为=14.368x+133.058.

    从而当x=2时，=161.794，当x=9时，=262.37.

    所以1998年污水排放量估计为161.794×108 t.

    2006年污水排放量预测为262.37×108 t.

    灵活选取数据可以简化运算，当只要求分析两变量相关关系，从而解决实际问题时，可选取恰当的变量进行分析.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013年海南省琼海市高考模拟测试文科数学试卷（解析版） 题型：解答题

    下表是我国2010年和2011年2～6月CPI同比（即当年某月与前一年同月相比）的增长数据，其中2011年的5个CPI数据成等差数列.

    （Ⅰ）求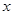、、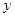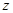的值；

    （Ⅱ）求2011年2～6月我国CPI数据的方差；

    （Ⅲ）一般认为，某月CPI数据达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点为严重通货膨胀，现随机从2010年5个月和2011年5个月的数据中各抽取一个数据，求相同月份2010年通货膨胀，并且2011年严重通货膨胀的概率.

    我国2010年和2011年2～6月份的CPI数据（单位：百分点，1个百分点 ）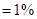

    年份

    二月

    三月

    四月

    五月

    六月

    2010

    2.7

    2.4

    2.8

    3.1

    3.9

    2011

    4.9

    5.0

     

    查看答案和解析>>

    科目：高中数学 来源：2013届广东省高二下学期期中文科数学试卷（解析版） 题型：解答题

    下表是我国一个工业城市每年中度以上污染的天数，由于以前只注重经济发展，没有过多的考虑工业发展对环境的影响，近几年来，该市加大了对污染企业的治理整顿，环境不断得到改善。

    年份（x）

    2005年

    2006年

    2007年

    2008年

    2009年

    中度以上污染的天数(y)

    90

    74

    62

    54

    45

    （1）请根据上表提供的数据，用最小二乘法求出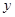关于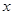的线性回归方程；

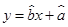    （2）按照环境改善的趋势，估计2012年中度以上污染的天数。

    （3）在以上5年中任取2年，至少有1年中度以上污染的天数小于60天的概率有多大。

    （可用公式，     ）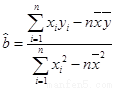

     

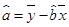    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面是我国居民生活污水排放量的一组数据:

    年份

    1995

    1996

    1997

    1998

    1999

    2000

    2001

    2002

    排放量

    151

     

    189.1

    194.8

    203.8

    220.9

    227.7

    232.3

        试估计1996年我国居民生活污水排放量,并预测2003年生活污水排放量(单位:108t).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面是我国居民生活污水排放量的一组数据，估计2000年的我国居民生活污水排放量，并预测2007年生活污水排放量(单位：亿立方米).

    年份        排放量

    1999          151

                          2000

    2001         189.1

    2002          194.8

    2003          203.8

    2004          220.9

    2005          227.7

    2006          232.3

    查看答案和解析>>

    同步练习册答案