
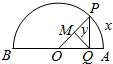
 如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )| A. |  | B. | 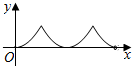 | C. |  | D. | 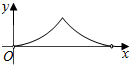 |
分析 在直角三角形OQP中,求出OQ,注意长度、距离为正,再根据直角三角形的锐角三角函数的定义即可得到f(x)的表达式,然后化简,分析周期和最值,结合图象正确选择.
解答 解:在直角三角形OQP中,设OP=1,
∵弧AP的长为x,则∠POQ=x,OQ=|cosx|,
∴点Q到直线OP的距离即QM=y,
∴y=f(x)=OQ|sinx|=|cosx|•|sinx|=$\frac{1}{2}$|sin2x|,
其周期为T=$\frac{π}{2}$,最大值为$\frac{1}{2}$,最小值为0,
故选A.
点评 本题主要考查三角函数的图象与性质,正确表示函数的表达式是解题的关键,同时考查二倍角公式的运用.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:选择题
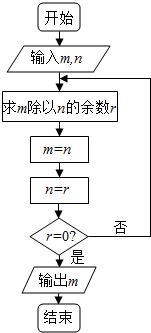 如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )| A. | 0 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{π}{6}})$ | B. | $({\frac{π}{6},\frac{π}{4}})$ | C. | $({\frac{π}{4},\frac{π}{3}})$ | D. | $({\frac{π}{3},\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
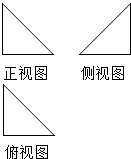 一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )
一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )| A. | 3π | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com