
已知数列{an}各项均为正数,Sn为其前n项和,对于 ,总有
,总有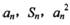 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II )设数列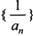 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: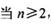
 时,
时,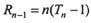 ;
;
(III)对任意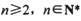 ,试比较
,试比较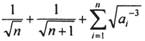 与
与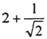 的大小
的大小
(I)an=1+(n-1)·1=n (n∈N*).(2)略 (3)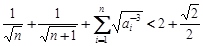
【解析】(I )由条件得 ,递写相减得an+1-an=1,由等差数列求得通项;(II )求出两边表达式证明相等;(III)数学归纳法或不等式证明。
,递写相减得an+1-an=1,由等差数列求得通项;(II )求出两边表达式证明相等;(III)数学归纳法或不等式证明。
解:(I)由题意,得 (n∈N*).
(n∈N*).
于是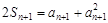 ,
,
两式相减,得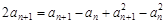 ,
,
即an+1+an=(an+1+an)(an+1-an),
由题,an>0,an+1+an≠0,
得an+1-an=1,即{an}为公差为1的等差数列.
又由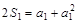 ,得a1=1或a1=0(舍去).
,得a1=1或a1=0(舍去).
∴ an=1+(n-1)·1=n (n∈N*).……………………………………………5分
(II)证法一:由(I)知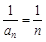 ,于是
,于是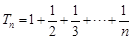 ,
,
于是当n≥2时,
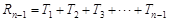 =
=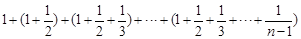
=
=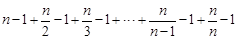
=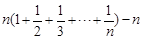 =n(Tn-1). ……………………………10分
=n(Tn-1). ……………………………10分
法二:①当n=2时,R1=T1= =1,2(T2-1)=2(
=1,2(T2-1)=2(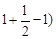 =1,
=1,
∴ n=2时,等式成立.
②假设n=k(k≥2)时,等式成立,即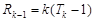 ,
,
当n=k+1时,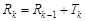
=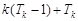 =
=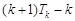 =
=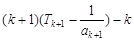
=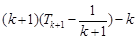 =
=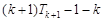 =
=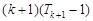 .
.
∴ 当n=k+1时,等式也成立.
综合①②知,原等式对n≥2,n∈N*均成立. …………………………10分
(III)由(I)知,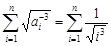 .
.
由分析法易知,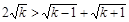 ,
,
当k≥2时,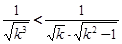
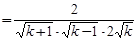
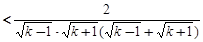
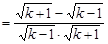
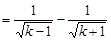 ,∴
,∴ 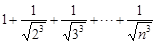
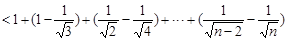
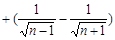
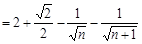 .即
.即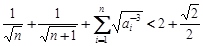 .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3an | ||
2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
1+
| ||||||
| 2nSn |
| lim |
| n→∞ |
| f(n+1) |
| f(n) |
| p+1 |
| 2p |
| f(n+1) |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | 2 n |
| an |
| 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com